Рассмотрим следующую игру, которую, по данным автора книг о математике Мартина Гарднера, изобрели в 1958 году два друга — Джон Г. Фокс и Л. Джеральд Марни
[116]. Попросите кого-либо взять сколько угодно листов бумаги и написать на каждом из них разные положительные числа — любые, от крохотных дробей до невероятно огромного числа, скажем 1 с сотней нулей. Затем листы бумаги следует положить на стол числами вниз и перемешать. Теперь начинается игра. Вы переворачиваете листы один за другим. Ваша задача — остановиться в тот момент, когда перевернете лист с самым крупным числом. Не разрешается возвращаться и выбирать число на листе, который вы уже перевернули. Если вы продолжаете переворачивать листы до самого конца, то сможете выбрать только число на последнем из них.
Поскольку игрок, переворачивающий листы бумаги, не знает, какие числа на них написаны, на первый взгляд может показаться, что его шансы выиграть невелики. Однако что поразительно, в эту игру можно выиграть более чем в трети случаев, независимо от того, сколько листов бумаги в ней задействовано. Вся хитрость — в умелом использовании информации об уже увиденных числах, для того чтобы сделать определенный вывод о числах на листах, которые еще не перевернуты. Стратегия состоит вот в чем: переверните определенное количество листов бумаги, выберите в качестве критерия сравнения максимальное число из уже открытых, а затем остановитесь на первом же числе, превышающем это значение. На самом деле оптимальное решение — перевернуть
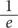 (0,368, или 36,8 процента) от общего количества листов бумаги, а затем выбрать первое число, которое больше любого другого числа среди уже перевернутых листов. В этом случае вероятность того, что вы найдете максимальное число, составляет
(0,368, или 36,8 процента) от общего количества листов бумаги, а затем выбрать первое число, которое больше любого другого числа среди уже перевернутых листов. В этом случае вероятность того, что вы найдете максимальное число, составляет
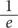 , или 36,8 процента.
, или 36,8 процента.
В 1960-х годах эта головоломка получила известность под названием «задача о выборе секретаря», или «задача о браке», поскольку она аналогична ситуации, когда босс просматривает список кандидатов на должность секретаря или мужчина анализирует список потенциальных жен, решая, как определить самую лучшую из имеющихся кандидатур
[117]. (А еще причина такого названия, по всей вероятности, связана с тем, что большинство математиков — мужчины.)
Представьте себе, что вы проводите собеседования с двадцатью претендентами на должность вашего секретаря, причем решение относительно каждого кандидата должны принимать сразу. Если вы предложите это место первому же соискателю, то не поговорите со всеми остальными, а если никого не выберете до самого последнего претендента, то вам придется отдать эту работу именно ему. Или представьте, что вы намерены назначить свидание двадцати женщинам, зная, что на каждом очередном свидании вам предстоит решать, ваша ли это избранница, прежде чем назначать свидание следующей женщине. (Приношу свои извинения читательницам. Данная аналогия основана на предположении о том, что мужчина делает предложение женщине, а женщина обязательно отвечает согласием.) Если вы сделаете предложение на первом свидании, вы не сможете встретиться со всеми остальными женщинами, а если побываете на свидании с каждой из них, вам придется сделать предложение последней женщине, с которой вы встретитесь. В обоих случаях лучший способ увеличить вероятность выбора самой подходящей кандидатуры — провести собеседования с 36,8 процента кандидатов, а затем предложить работу или руку и сердце тому из них, кто окажется лучшим из тех, с кем вы уже пообщались. Этот метод не гарантирует, что вы найдете наиболее оптимальный вариант (вероятность всего 36,8 процента), но это все равно лучшая стратегия.
Если бы Кеплер знал в свое время, что ему предстоит общение с одиннадцатью женщинами, и применил эту стратегию, он встретился бы с 36,8 процента из них (четырьмя), а затем сделал бы предложение той из оставшихся кандидаток, которая понравилась бы ему больше тех, кого он уже видел. Другими словами, он выбрал бы пятую женщину, что он действительно сделал, но только после того, как встретился со всеми одиннадцатью претендентками (и этот брак оказался счастливым). Если бы Кеплер знал решение задачи о браке, он избавил бы себя от шести неудачных свиданий.
Задача о выборе секретаря (или задача о браке) стала одной из самых знаменитых в занимательной математике, хотя она и не отображает реальность, поскольку боссы могут вызывать кандидатов повторно, а мужчины — возвращаться к тем женщинам, с которыми встречались ранее (как и сделал Кеплер). Тем не менее в основе ее решения лежит невероятно полезная теория, получившая название «оптимальная остановка», другими словами — математическое обоснование того, когда лучше всего остановиться. Решение задачи об оптимальной остановке играет важную роль в сфере финансов, позволяя, например, определить, когда пора ограничить убытки по инвестициям или исполнить фондовый опцион. А еще оно может пригодиться в таких областях, как медицина (скажем, чтобы рассчитать оптимальное время для прекращения того или иного курса лечения), энергетика (чтобы составить прогноз, когда не стоит полагаться на углеводородное топливо), зоология (чтобы установить, когда закончить исследование большой популяции животных в поисках новых видов, которых там, похоже, нет, тем самым избежав напрасной траты средств).
Российский олигарх Борис Березовский был в прошлом профессором математики Академии наук СССР, которая стала преемницей альма-матер Эйлера
[118] В 1980-х годах в соавторстве с другим ученым Березовский написал книгу, посвященную задаче о выборе секретаря. В 2003 году он переехал в Великобританию. Я несколько раз обращался к Борису Березовскому с просьбой о встрече, но всякий раз он просил меня перезвонить через пару месяцев. Через год безуспешных попыток я понял, что пора остановиться.



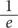 (0,368, или 36,8 процента) от общего количества листов бумаги, а затем выбрать первое число, которое больше любого другого числа среди уже перевернутых листов. В этом случае вероятность того, что вы найдете максимальное число, составляет
(0,368, или 36,8 процента) от общего количества листов бумаги, а затем выбрать первое число, которое больше любого другого числа среди уже перевернутых листов. В этом случае вероятность того, что вы найдете максимальное число, составляет
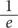 , или 36,8 процента.
, или 36,8 процента.