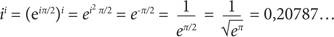Эти формулы можно записать так:
b = r sin θ; a = r cos θ
Следовательно, наше комплексное число может быть выражено через r и θ:
a + bi = r cos θ + (r sin θ) i
a + bi = r cos θ + ri sin θ
a + bi = r (cos θ + i sin θ)
Но постойте! Мы ведь знаем, что cos θ + i sin θ = eiθ. Следовательно, мы можем заменить те члены уравнения, которые стоят в скобках, и получить такую формулу:
a + bi = reiθ
Попытайтесь прочувствовать это уравнение. Комплексное число, которое находится на расстоянии r от начала координат, под углом θ радиан по отношению к горизонтальной оси, имеет форму reiθ. Немного выше в этой главе я задал вопрос, что значит число е в мнимой степени, но тогда это казалось непонятным. Сейчас мы нашли на него ответ. Когда число е имеет мнимую степень, такой член представляет собой невероятно эффективное обозначение позиции на комплексной плоскости.
Теперь давайте рассмотрим точку на комплексной плоскости с координатами (–1, 0), которая представляет комплексное число –1 + 0i, или просто −1. Как показано на рисунке ниже, эта точка находится на расстоянии в 1 единицу от начала координат под углом в π радиан, а значит, мы можем записать ее как eiπ.
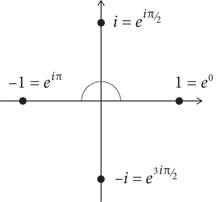
Мы с вами заново открыли тождество Эйлера! Формула, описывающая позицию точки −1 на комплексной плоскости, выглядит следующим образом:
— 1 = eiπ
Это уравнение можно преобразовать в такую форму:
eiπ + 1 = 0
Кроме того, поскольку точка i расположена на расстоянии в 1 единицу от начала координат под углом π/2 радиан к горизонтали, мы можем сделать вывод, что i = eiπ/2, а так как −i находится на расстоянии в 1 единицу от начала координат под углом 3π/2 радиан, напрашивается вывод, что −i = e3iπ/2.
Сделайте глубокий вдох. Сейчас мы используем эту информацию, чтобы ответить на потрясающий вопрос, который еще несколько страниц назад мог бы показаться полным бредом, граничащим с безумием: что представляет собой ii, или квадратный корень из минус единицы в степени квадратный корень из минус единицы?
Поскольку мы знаем, что eiπ/2 = i, мы знаем также, что:
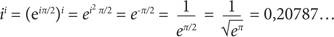
Здесь i исчезает, оставляя после себя такое число, которое поняли бы даже древние греки. Только представьте себе!
Комплексная плоскость позволяет забыть беспокойную мысль о том, что i — это квадратный корень из отрицательного числа. Мы должны помнить только то, что комплексное число a + bi представляет собой точку на плоскости с координатами (a, b), где a и b — действительные числа, а также что сложение или умножение этих координат подчиняется определенным правилам. (Разумеется, эти правила основаны на свойствах квадратного корня из минус единицы, но сейчас нас должно интересовать не то, как они появились, а в чем их суть.) Вскоре математики задумались над тем, можно ли создать такие же правила для трехмерной системы координат, что позволило бы описывать вращения в пространстве подобно тому, как правила для комплексных чисел описывают вращения в двумерной системе координат. Больше всех проникся этой идеей ирландский математик Уильям Роуэн Гамильтон, но ему не удавалось найти ответ. И вот однажды в 1843 году, когда Гамильтон прогуливался с женой вдоль Королевского канала в Дублине, на него снизошло озарение, которое вылилось в знаменитый математический акт вандализма: Гамильтон нацарапал на стене моста Брумбридж такую формулу: i2 = j2 = k2 = ijk = –1. Сейчас на этом месте установлена памятная табличка.
Гамильтон понял, что невозможно найти математически допустимые правила для координат с тремя числами, но их можно применить для четырех чисел. Он назвал свое открытие «кватернионы». Подобно тому как комплексное число a + bi (где a и b — действительные числа, а i — √−1) можно представить в виде точки на плоскости с координатами (a, b), кватернион a + bi + cj + dk, где a, b, c и d — действительные числа, а i, j и k равны √–1, можно записать с помощью координат (a, b, c, d). Хотя каждая из мнимых единиц i, j и k равна √–1, все же они разные, как следует из уравнения, записанного Гамильтоном на кирпичной кладке моста. Для того чтобы кватернионы работали, Гамильтону понадобилось еще одно странное правило, которое гласит, что порядок умножения мнимых единиц имеет значение. Например, i × j = k, но j × i = —k.
Кватернионы Гамильтона представляли собой весьма необычную концепцию, но все же позволили ему создать модель вращений в трехмерном пространстве. В кватернионе (a, b, c, d) числа (b, c, d) — это три координаты для трех размерностей пространства, тогда как число а отображает время. Эти новые числа так взволновали Гамильтона, что он посвятил их изучению большую часть оставшейся жизни.
Если концепция кватернионов кажется вам несколько странной, вы в этом не одиноки. Современники Гамильтона высмеяли его, и особенно Чарльз Доджсон, математик из Оксфордского университета, больше известный как Льюис Кэрролл. Его книги для детей «Алиса в Стране чудес» и «Алиса в Зазеркалье» славятся своими логическими головоломками и математическими играми. Однако совсем недавно один критик заявил, что в основе сюрреалистического юмора этих книг лежит не богатое воображение Доджсона, а его желание поглумиться над изменениями в математике викторианской эпохи, которых он не одобрял, что больше всего касалось тенденции к повышению уровня абстракции в алгебре. Мелани Бейли написала в своей статье, что глава A Mad Tea Party («Безумное чаепитие») — это сатира на кватернионы Гамильтона, и даже само название представляет собой игру слов, поскольку его можно интерпретировать как mad t-party, где t — научный символ для обозначения времени
[135]. За чаепитием Безумный Шляпник, Мартовский Заяц и Мышь Соня вращаются вокруг стола, подобно мнимым числам i, j и k в кватернионе. Четвертый гость по имени Время отсутствует, поэтому на мытье посуды времени нет. Когда Мартовский Заяц сказал Алисе, чтобы она говорила то, что думает, Алиса ответила: «…Во всяком случае… что я думаю, то и говорю. В общем, это ведь одно и то же!» Но порядок слов в предложении все же меняет смысл, точно так же как порядок умножения i и j меняет результат.