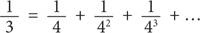
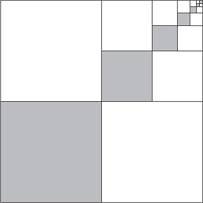
Посмотрите на этот рисунок и попытайтесь понять почему. (А если не сможете, откройте Приложение 6.) Если это уравнение верно, тогда общая площадь равна:
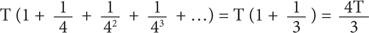
Что и требовалось доказать.
Квадратура параболы Архимеда — самый наглядный пример применения метода последовательных исчерпываний: суммирование последовательности площадей малых фигур, приближающихся к площади большой фигуры. Доказательство этого метода считается наиболее значительным достижением Архимеда, поскольку отображает первую «современную» трактовку математической бесконечности. За две сотни лет до Архимеда философ Зенон предостерегал против использования такого понятия, как бесконечность, в серии парадоксов. В самом знаменитом из них, «Ахиллес и черепаха», демонстрировалось, что сложение бесконечного количества величин приводит к абсурдному результату.
Представьте себе, говорил Зенон, что Ахиллес пытается догнать черепаху. Когда атлет достигнет того места, где она была, когда он начал свой бег, черепаха проползет немного дальше. Когда он доберется до второй позиции, черепаха снова продвинется дальше. Ахиллес может продолжать свой бег сколько угодно, но каждый раз, когда он будет достигать того места, где находилась черепаха, она уже будет немного впереди. Зенон утверждал, что если рассматривать движение как бесконечное количество рывков на протяжении бесконечного количества интервалов, то быстроногий Ахиллес никогда не догонит неповоротливую черепаху. Древние греки так и не смогли развязать логические узлы Зенона, поэтому математики всячески избегали концепции бесконечности в своей работе. Даже Архимед, использовавший метод последовательных исчерпываний, никогда не называл всеобъемлющую сущность именем «бесконечный ряд» так прямо, как это делаю я. Но различия касались исключительно терминологии, а не самой идеи. Архимед был первым мыслителем, создавшим аппарат для работы с бесконечным рядом, имеющим конечный предел. Это было важно не только для покорения площадей гораздо более сложных фигур, чем парабола, но и для начала концептуального пути к исчислению. Архимед стал первым из тех атлантов, на плечи которых обопрется в свое время Исаак Ньютон.
Если бесконечность — это самое большое число, тогда какое число самое маленькое? В XVII столетии математики ввели новую концепцию под названием «бесконечно малая величина» — величина, которая меньше любой другой действительной величины, но все же больше ноля.
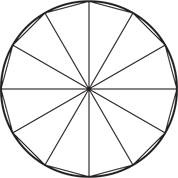
Бесконечно малая величина была и чем-то, и ничем: достаточно большая для применения в математике, но и достаточно малая, чтобы исчезнуть, когда вам это необходимо. Рассмотрим в качестве иллюстрации окружность, изображенную на рисунке ниже. В нее вписан двенадцатиугольник — фигура с 12 сторонами, состоящая из 12 идентичных треугольников с общей вершиной, совокупная площадь которых примерно равна площади круга. Если я построю в этой окружности многоугольник с большим числом сторон, содержащий большее количество более узких треугольников, их совокупная площадь еще сильнее приблизится к площади круга. Если я продолжу увеличивать количество сторон, в предельном случае я получу многоугольник с бесконечным количеством сторон, содержащих бесконечное количество бесконечно узких треугольников. Площадь каждого такого треугольника представляет собой бесконечно малую величину, но их совокупная площадь равна площади круга.
В предыдущих главах мы уже дважды встречались с немецким астрономом Иоганном Кеплером. Это именно он понял, что планеты движутся по эллиптическим орбитам, и это он побывал на одиннадцати свиданиях, прежде чем нашел вторую жену. Когда Кеплер сделал предложение будущей фрау К., оставался такой пустяк, как организация свадебной церемонии. Покупая вино, ученый увидел, что виноторговцы определяют объем полной бочки вина, вставляя в нее по диагонали прут через наливное отверстие, расположенное посредине боковой стороны бочки. Это был грубый, приближенный метод, и он совсем не понравился Кеплеру, поскольку прут одной и той же длины подходил для бочек разных размеров, как показано на рисунке ниже.
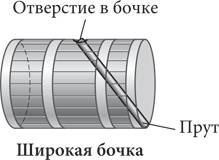

Измерение объема винных бочек
Кеплер начал размышлять над тем, как точнее вычислить объем бочки, для того чтобы определить, в бочке какой формы было бы больше всего вина при фиксированной длине прута
[143]. Вдохновленный идеями Архимеда, Кеплер разработал метод, в соответствии с которым разделил каждую бочку на бесконечное количество бесконечно малых фигур, объем которых можно было рассчитать. Затем он доказал, что для прута длиной l, проходящего от наливного отверстия до дальнего угла бочки, бочка будет иметь максимальный объем, если ее ширина равна
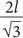 . Кеплер оказался первым представителем целого поколения математиков, использовавших бесконечно малые величины в процессе вычисления площадей и объемов. Среди математиков разных стран, от Англии до Италии, начался бурный рост активности в этой области, что отображало самый значительный сдвиг в математической культуре со времен древних греков — ярых приверженцев концепций, имеющих логический смысл. Теперь же логическая строгость была отброшена, уступив место тому, что давало результаты. Бесконечно малые величины представляли собой нечто неопределенное, что существовало и не существовало одновременно. Но никто не собирался отказываться от них.
. Кеплер оказался первым представителем целого поколения математиков, использовавших бесконечно малые величины в процессе вычисления площадей и объемов. Среди математиков разных стран, от Англии до Италии, начался бурный рост активности в этой области, что отображало самый значительный сдвиг в математической культуре со времен древних греков — ярых приверженцев концепций, имеющих логический смысл. Теперь же логическая строгость была отброшена, уступив место тому, что давало результаты. Бесконечно малые величины представляли собой нечто неопределенное, что существовало и не существовало одновременно. Но никто не собирался отказываться от них.
Бесконечно малые величины позволили разработать чрезвычайно эффективный метод определения касательной — линии, которая касается кривой в определенной точке, но не пересекает ее. Представьте, что нам необходимо найти касательную в точке Р к кривой, изображенной на рисунке ниже. Стратегия построения касательной состоит в том, чтобы провести приближенную прямую в соответствующей точке, а затем улучшать приближение до тех пор, пока она не совпадет с искомой прямой. Мы можем сделать это, нарисовав линию, проходящую через точку Р и пересекающую кривую в расположенной рядом точке Q, а затем смещать эту точку все ближе и ближе к точке Р. Когда точка Q совпадет с точкой Р, полученная линия будет касательной к данной кривой в точке Р.



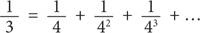
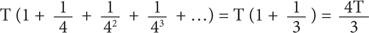




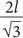 . Кеплер оказался первым представителем целого поколения математиков, использовавших бесконечно малые величины в процессе вычисления площадей и объемов. Среди математиков разных стран, от Англии до Италии, начался бурный рост активности в этой области, что отображало самый значительный сдвиг в математической культуре со времен древних греков — ярых приверженцев концепций, имеющих логический смысл. Теперь же логическая строгость была отброшена, уступив место тому, что давало результаты. Бесконечно малые величины представляли собой нечто неопределенное, что существовало и не существовало одновременно. Но никто не собирался отказываться от них.
. Кеплер оказался первым представителем целого поколения математиков, использовавших бесконечно малые величины в процессе вычисления площадей и объемов. Среди математиков разных стран, от Англии до Италии, начался бурный рост активности в этой области, что отображало самый значительный сдвиг в математической культуре со времен древних греков — ярых приверженцев концепций, имеющих логический смысл. Теперь же логическая строгость была отброшена, уступив место тому, что давало результаты. Бесконечно малые величины представляли собой нечто неопределенное, что существовало и не существовало одновременно. Но никто не собирался отказываться от них.