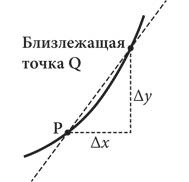
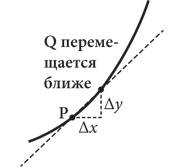
Аппроксимация касательной
Как мы уже знаем, градиент прямой линии — это отношение расстояния, покрытого прямой по вертикали, к расстоянию по горизонтали, а градиент кривой в определенной точке — это градиент касательной в этой точке. Касательные интересовали математиков только из-за градиентов. На представленном выше рисунке градиент линии, проходящей через точки P и Q, равен ∆y/∆x. (Греческая буква ∆ («дельта») — это математический символ, которым обозначаются малые приращения.) По мере приближения точки Q к точке Р значение ∆y/∆x приближается к градиенту касательной в точке Р. Но здесь возникает одна проблема. Если точка Q действительно совпадет с точкой Р, тогда ∆y = 0 и ∆x = 0, а это значит, что градиент кривой в точке Р равен 0/0. Но ведь это некорректная математическая операция! Арифметические правила запрещают деление на ноль! Проблему можно решить, удерживая точку Q на бесконечно малом расстоянии от точки Р. Сделав это, мы сможем сказать, что, когда точка Q приближается к точке Р на бесконечно малое расстояние, значение ∆y/∆x становится бесконечно близким к градиенту кривой в точке Р.
В 1665 году Исаак Ньютон, недавно окончивший Кембридж, вернулся в дом своей матери в Линкольншире
[144]. «Черная смерть» уничтожала город за городом по всей Британии. Университет закрыли, чтобы защитить его персонал и студентов. В доме матери Ньютон устроил себе небольшой кабинет и начал записывать свои математические идеи в огромный дневник, который назвал «черновиком». На протяжении следующих двух лет Ньютон вел образ жизни отшельника и, ни на что не отвлекаясь, вывел новые теоремы, которые легли в основу Philosophiae Naturalis Principia Mathematica
[145] — опубликованного в 1687 году трактата, изменившего наше понимание физической Вселенной в большей степени, чем любая другая работа до или после этой книги. В ней Ньютон описал систему законов природы, объясняющую, почему различные объекты, от падающих с дерева яблок до планет, вращающихся вокруг Солнца, двигаются именно так, а не иначе. Однако открытия, сделанные Ньютоном в физике, требовали столь же фундаментального прорыва в математике. Он формализовал работу по бесконечно малым величинам, выполненную за предыдущие полстолетия, объединив ее результаты в общую систему с унифицированными обозначениями. Ньютон назвал ее методом флюксий, но она получила известность под названием «исчисление бесконечно малых величин», а сейчас ее часто называют просто исчислением.
Движущееся тело меняет свое положение в пространстве, а его скорость представляет собой изменение этого положения во времени
[146]. Если тело перемещается с фиксированной скоростью, оно меняет свое положение на фиксированную величину за каждый промежуток времени. Движущийся с постоянной скоростью автомобиль, покрывающий 60 миль с 16 до 17 часов, движется со скоростью 60 миль в час. Ньютон хотел решить другую задачу: как вычислить скорость тела, перемещающегося не с постоянной скоростью? Предположим, тот же автомобиль движется не с постоянной скоростью 60 миль в час, а то ускоряет, то замедляет движение из-за транспортного потока. Один из методов расчета скорости этого автомобиля, например в 16:30, сводится к измерению отрезка пути, который он проедет с 16:30 до 16:31, что позволит определить расстояние, пройденное за минуту. (Для того чтобы получить скорость в милях в час, нам останется просто умножить это расстояние на 60.) Однако это значение представляет собой среднюю скорость за эту минуту, а не мгновенное значение скорости в 16:30. Мы можем взять еще более короткий промежуток, скажем путь, который проедет автомобиль с 16:30 до 16:30 и одна секунда, что даст нам расстояние за секунду. (Для того чтобы получить скорость в милях в час, необходимо умножить это расстояние на 3600.) Но это тоже всего лишь средняя скорость в данную секунду. Мы можем и дальше сокращать промежутки, но так и не получим мгновенное значение скорости до тех пор, пока этот промежуток не окажется меньше любого другого — другими словами, пока он не станем равным нулю. Но если промежуток равен нулю, автомобиль не движется!
Эта цепочка рассуждений должна показаться вам знакомой, поскольку я уже использовал ее выше, когда объяснял, как вычислить градиент точки на кривой. Для того чтобы определить градиент, мы делим бесконечно малую величину (длину) на другую бесконечно малую величину (еще одну длину). Для того чтобы вычислить мгновенное значение скорости, мы также должны разделить бесконечно малую величину (расстояние) на другую бесконечно малую величину (время). С математической точки зрения эти две задачи идентичны. Метод флюксий Ньютона был методом вычисления градиентов, который позволил рассчитывать мгновенное значение скорости движущихся объектов.
Посмотрим, как Ньютон применил этот метод для вычисления градиента кривой y = x2 — давно знакомой нам параболы. Изложенные ниже объяснения носят специальный характер, но, если вы будете читать медленно, вам не трудно будет их понять. К концу вы увидите, как Ньютон использовал бесконечно малые величины для выведения формулы градиента каждой точки на этой прямой.
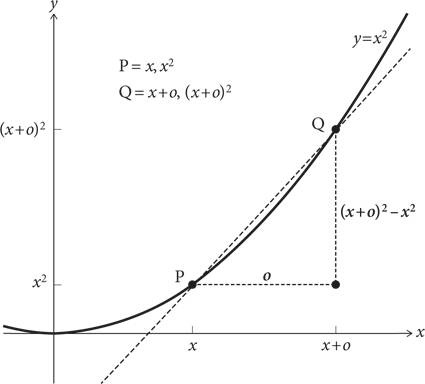
Вычисление градиента кривой y = x2
Для начала выполним те же действия, что и немного выше, в процессе построения касательной: возьмем произвольную точку Р, построим в ней приближенную касательную, которая проходит через другую точку Q, расположенную недалеко от Р вдоль кривой. Затем приблизим точку Q на бесконечно малое расстояние от Р. Градиент касательной в точке Р — и есть градиент кривой в этой точке. Давайте введем новый символ о и обозначим им расстояние по горизонтали между точками Р и Q, как показано на рисунке выше. Если координаты точки Р — (x, x2), то координаты точки Q — (x + o, (x + o)2). Следовательно, вертикальное расстояние между точками P и Q составляет (x + o)2 − x2, стало быть, градиент прямой равен отношению расстояния по вертикали к расстоянию, покрытому по горизонтали:






