Бывает, что достаточное время – это миллионная доля секунды. Электрон недолго пребывает в возбужденном состоянии, будучи в атоме. Итак, что должно произойти, когда электрон опускается на более низкий энергетический уровень? Он должен испустить фотон – новый, но с той же энергией, которую принял с предыдущим фотоном. При переходе на более высокий энергетический уровень фотон поглощается. При переходе на более низкий энергетический уровень фотон излучается, как показано волнистой стрелкой на рис. 6.1. Согласно знаменитому уравнению Эйнштейна, энергия E этого фотона равна hν, где h – постоянная Планка, а ν – частота фотона. Энергия излученного фотона в точности равна разнице между двумя энергетическими уровнями ΔE.(Заглавная греческая буква «дельта», Δ, часто используется для обозначения разницы или изменения величины). В результате получаем тождество ΔE = hν, позволяющее вычислить частоту того фотона, который был излучен электроном, когда тот опустился со второго на первый энергетический уровень.
Вы когда-нибудь играли с фосфоресцирующими фрисби? Чтобы они светились в темноте, их сначала нужно подержать на свету. Например, подвесить перед лампочкой. Что при этом происходит? Электроны в атомах и молекулах игрушки переходят на более высокие энергетические уровни (в таких сравнительно больших атомах много энергетических уровней) и поглощают фотоны света. Создатели игрушки подобрали такой материал, в котором эти электроны каскадируют не сразу, а постепенно, излучая при этом видимый свет. Конечно, такой процесс продолжается не вечно. Свечение прекращается после того, как все электроны вернутся в исходное состояние. Фосфоресцирующие фрисби и светящиеся костюмы скелетов, которые так нравятся детям, светятся благодаря одному и тому же принципу.
Энергия, поглощаемая электроном, может поступить от фотона, но бывают и другие источники энергии. Возможно, пролетающий мимо атом ударит по электрону, и электрон в результате такого воздействия будет заброшен на более высокий энергетический уровень. В данном случае переход осуществляется за счет кинетической энергии. Как подобный механизм работает в облаке газообразного водорода? Во-первых, нужно выяснить, а какова температура этого водородного облака? Температура в кельвинах пропорциональна средней кинетической энергии молекул или атомов в облаке. Переносное движение облака не влияет на эти измерения. Естественно, кинетическая энергия – это энергия движения, поэтому чем выше температура, тем быстрее эти частицы носятся взад-вперед. Если бы я был электроном в основном состоянии и мне дали под зад, то я мог бы проверить энергию этого пинка. Если бы такого пинка хватило, чтобы я пролетел лишь часть пути до второго энергетического уровня, то я остался бы на месте. Но если энергия пинка именно такая, какая нужна для перехода на второй энергетический уровень, то я приму эту энергию, поглощу ее и перейду на второй уровень.
При достаточной температуре можно обеспечить, чтобы вся совокупность атомов и некоторая доля их электронов находились в сравнительно высоком состоянии. Можно поддерживать такое равновесие, так, чтобы любой упавший электрон сразу выталкивался на уровень выше. Примерно так действует жонглер, удерживающий несколько мячиков в воздухе. Все это – функция температуры. При низких температурах абсолютное большинство электронов остается на энергетическом уровне n = 1 и лишь немногие электроны – на энергетическом уровне n = 2. По мере повышения температуры все больше электронов выталкивается на энергетический уровень n = 2.
Резюме. Допустим, межзвездное газовое облако подсвечивается сиянием звезды, температура которой составляет 10 000 К. У большинства атомов – множество очень сложных энергетических уровней, таково устройство природы; энергетические уровни водорода при этом сравнительно просты. Эта разнородная смесь совершенно искажает чистый тепловой спектр, излучаемый звездой с температурой 10 000 К. Посмотрим, какой же хаос получается.
Во-первых, рассмотрим полноценный атом водорода. В нем – бесконечное количество энергетических уровней, соответствующих концентрическим орбиталям, расположенным все дальше и дальше от ядра: n = 1 (основное состояние; ближайшая к ядру орбиталь), n = 2 (первый уровень возбуждения), n = 3, n = 4, n = 5, n = 6 … n = ∞. Схема энергетических уровней напоминает лестницу, поэтому называется «лестничная диаграмма». Нижние энергетические уровни, расположенные на которых электроны теснее связаны с ядром, на диаграмме также располагаются внизу (рис. 6.2).
Первое возбужденное состояние водорода – n = 2, на три четверти пути вверх, за ним следует n = 3, затем n = 4, n = 5 и так далее. Электрон с высоким n занимает очень высокую орбиталь и имеет очень слабую связь с протоном. На самом верху диаграммы энергия связи электрона равна нулю. Энергия в атомах измеряется в электрон-вольтах, эВ. Это энергия, требуемая электрону, чтобы преодолеть разность потенциалов в 1 вольт. Допустим, у вас есть фонарик, работающий от девятивольтной батарейки. Каждый электрон, проходя по проводам в фонарике, генерирует 9 эВ энергии в виде света и теплоты. По проводам фонарика может проходить 6,24 × 1018 электронов в секунду, при этом будет генерироваться энергия в 9 × (6,24 × 1018) эВ (или 9 ватт) световой и тепловой энергии в секунду. Следовательно, один электрон-вольт – очень малая энергия; просто такими единицами удобно оперировать, когда речь идет о небольших порциях энергии, обмен которыми происходит при электронных переходах. Например, –13,6 эВ на рисунке соответствует энергетическому уровню n = 1. Эта энергия показана как отрицательная. Чтобы вывести этот электрон из атома, ему нужно сообщить энергию 13,6 эВ. Говорят, что 13,6 эВ – это энергия связывания для основного состояния электрона n = 1. Что будет, если электрон в основном состоянии заметит фотон с энергией более 13,6 эВ? Он сможет поглотить этот фотон? Вот фотон с таким количеством энергии, что электрону с ним делать? Если электрон поглотит такой фотон, то ему хватит энергии, чтобы заскочить выше n = ∞. Что выше n = ∞? Свобода. Если электрон выскочит туда на уровень энергии выше нуля, то покинет атом и расстанется со своим протоном. В таком случае мы ионизируем атом – оторвем у него электрон.
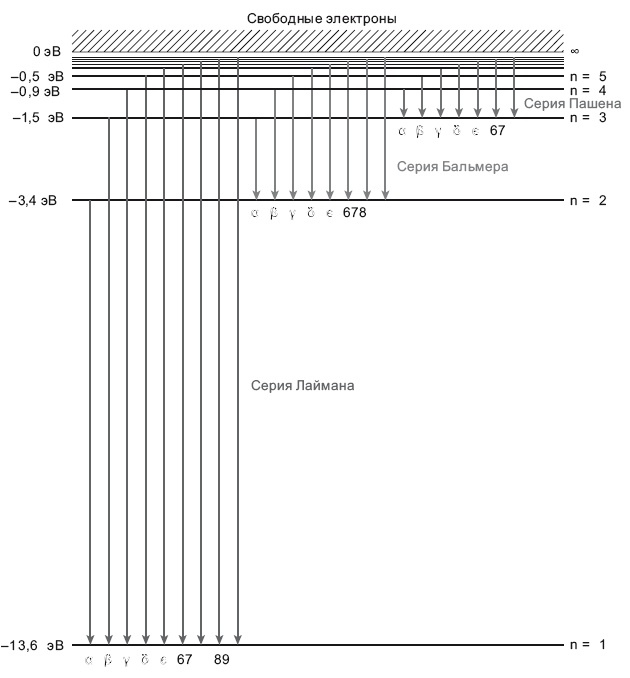
Рис. 6.2. Схема энергетических уровней водорода. Горизонтальными линиями обозначены различные энергетические уровни в атоме водорода в электрон-вольтах (эВ). Стрелками обозначены переходы электрона, при которых он может перескочить с одного энергетического уровня на другой, излучая фотон, энергия которого равна разности потенциалов между этими уровнями. Показаны переходы на первый энергетический уровень (серия Лаймана, где излучаются фотоны в ультрафиолетовой части спектра), на второй энергетический уровень (серия Бальмера, где излучаются фотоны видимого света) и на третий уровень (серия Пашена, ближний инфракрасный диапазон). На схеме показано, как электроны спускаются между энергетическими уровнями и излучают фотоны. Если электрон был на энергетическом уровне n = 3 и опустился на энергетический уровень n = 2, то он испустит фотон Hα (серия Бальмера) с энергией 1,9 эВ.



