Почему Эйнштейн поверил во второй постулат? Потому, что скорость света в уравнениях Максвелла являлась постоянной и была связана с соотношением магнитных и электрических сил, которые можно измерить в лаборатории. Максвелл вычислил, что волны света распространяются в вакууме со скоростью около 300 000 км/c. Если бы вы зафиксировали луч света, летящий с другой скоростью – например, 200 000 км/c, – то могли бы логически заключить, что движетесь со скоростью 100 000 км/c, вообще понять, что движетесь. Это противоречило бы первому постулату. В 1887 году Альберт Майкельсон и Эдвард Морли поставили знаменитый эксперимент, при котором пытались измерить скорость Земли, вращающейся вокруг Солнца, по отражению солнечных лучей от установленных в лаборатории зеркал. Фактически они измеряли разницу скоростей света относительно своей лаборатории для лучей, летящих параллельно и перпендикулярно вектору скорости Земли. Они добились достаточной чувствительности эксперимента для измерений на скорости 30 км/c, с которой Земля движется вокруг Солнца. Удивительно, но скорость Земли у них получилась нулевой, как если бы Земля была неподвижной, а лучи света относительно их лаборатории летели бы во всех направлениях с одинаковой скоростью. Но именно такой результат они и должны были получить в соответствии со вторым постулатом Эйнштейна. Измеренная вами скорость света всегда будет одинакова, независимо от того, движется Земля или нет. Следовательно, если вы верите во второй постулат, то могли бы спрогнозировать, что Майкельсон и Морли зафиксируют в своем эксперименте нулевую скорость.
Итак, Эйнштейн решил поверить в два своих постулата и доказывать теоремы, исходя из них. Вот один из его выводов: нельзя сконструировать ракету, развивающую сверхсветовую скорость. Почему так? Допустим, я направляю лазерный луч на стену комнаты; он достигает стены. Я могу полагать, что нахожусь в состоянии покоя. Но если сконструировать ракету, развивающую сверхсветовую скорость, и повторить у нее на борту тот же эксперимент, то результат будет иным. Если вы находитесь в центре ракеты и направляете лазер в ее носовую часть, то свет туда никогда не долетит. Любой спортсмен вам скажет, что нельзя догнать соперника, который бегает быстрее вас и опережал вас на старте. Лазерный луч никогда не долетит до носовой части ракеты, так как носовая часть летит быстрее него (быстрее света) и стартовала раньше. Естественно, если бы вы поставили такой эксперимент в корпусе ракеты, то лазер никогда не достиг бы ее носовой части, и вы бы знали, что движетесь (на самом деле быстрее света). Но подождите – это противоречит первому постулату. Поскольку вы летите с постоянной скоростью в одном и том же направлении, вы никак не можете доказать, что движетесь. Ваш эксперимент должен дать тот же результат, что и эксперимент у меня в комнате. Следовательно, невозможно сконструировать ракету, развивающую сверхсветовую скорость. Странный результат, но с ним придется согласиться, если вы согласны с двумя постулатами. Если ракета летит медленнее скорости света, то лазерный луч рано или поздно попадет в ее носовую часть. На это может уйти немало времени, но, например, если ваши часы идут достаточно медленно, то все получится. Летать со субсветовой скоростью можно, но нельзя сконструировать ракету, развивающую сверхсветовую скорость. Этот тезис был проверен на ускорителях частиц, где протоны и электроны разгоняют все сильнее и сильнее, они развивают скорости все ближе и ближе к световой, но скорости света так и не достигают.
Вот другой результат. Вообразите себе «светочасы», устройство, в котором луч света отражается по вертикали между двумя зеркалами, одно из которых расположено, скажем, на потолке, а второе на полу. Каждое отражение – это такт часов. Скорость света равна 300 000 километров в секунду или примерно 30 см в наносекунду. Одна наносекунда – это миллиардная часть секунды. Если расположить два зеркала на расстоянии всего 90 см, то часы будут тикать с частотой раз в 3 наносекунды (рис. 17.1).
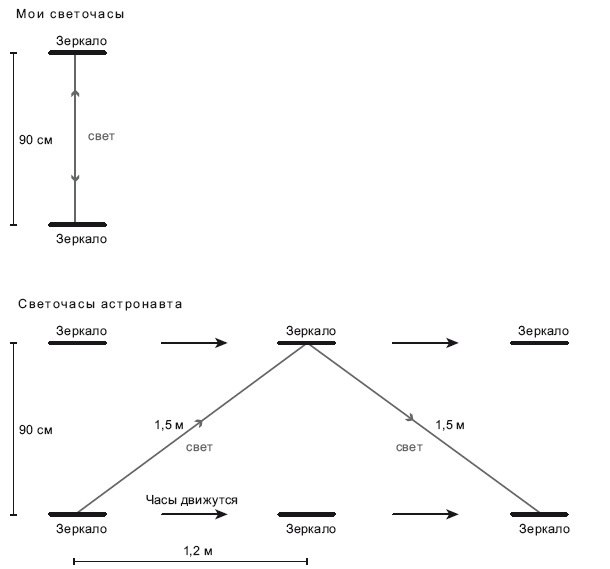
Рис. 17.1. Светочасы. Мои светочасы тикают каждые 3 наносекунды. Аналогичные светочасы взял с собой астронавт, корабль которого летит относительно меня со скоростью 80 % от световой. Свет движется с постоянной скоростью: 30 сантиметров в наносекунду. Я вижу, как лучи света от часов астронавта летят по длинным полутораметровым диагональным отрезкам и, следовательно, мне кажется, что светочасы астронавта тикают каждые 5 наносекунд. Иллюстрация предоставлена Дж. Ричардом Готтом, адаптирована из Time Travel in Einstein’s Universe, Houghton Mifflin, 2001
Это очень быстрые часы. По конструкции похожи на стоячие часы с маятником, только очень быстрые. Свет будет отражаться между двумя зеркалами туда-сюда, туда-сюда. На моих светочасах он будет попадать в зеркало каждые 3 наносекунды. А теперь представьте себе астронавта, летящего на ракете со скоростью 80 % от световой и взявшего с собой аналогичные светочасы (рис. 17.1). Он летит медленнее скорости света, так что опыт сработает. С точки зрения астронавта, его часы тикают нормально, свет преодолевает путь от зеркала до зеркала за 3 наносекунды. Но если я загляну в иллюминатор его ракеты, то увижу, что его часы летят вместе с ракетой на скорости 80 % от световой, а луч света в них летит по диагональной траектории. Луч света летит снизу, но к тому времени, как он преодолеет 90 см, верхнее зеркало уже успеет сдвинуться вправо на 120 см. Свет летит по диагональной траектории, состоящей из отрезков по 150 см. Получается прямоугольный треугольник со сторонами 3–4–5: 90 см по вертикали, 120 см слева направо и гипотенуза длиной 150 см. Треугольник удовлетворяет теореме Пифагора: 32 + 42 = 52. Тогда как относительно меня свет проходит 150 см по диагонали из левой нижней точки в правую верхнюю, с точки зрения астронавта свет преодолевает 120 см слева направо. Следовательно, астронавт движется относительно меня с 4/5, или 80 %, скорости света. Поскольку мне должно казаться (согласно второму постулату), что луч света преодолевает 30 см в наносекунду, я должен сказать, что свет успевает пройти отрезок диагональной траектории длиной 150 см, из нижней точки слева в верхнюю точку справа. Именно это я и наблюдаю. Еще через 5 наносекунд он вновь опустится по диагонали и попадет в нижнее зеркало на 240 см правее, нежели в начале предыдущего отскока. Соответственно я должен сказать, что часы астронавта тикают с частотой раз в 5 наносекунд, а не раз в 3 наносекунды. Мне кажется, что его часы идут медленнее моих со скоростью 3/5 по отношению к ним.
Теперь переходим к самому интересному. Мне должно казаться, что и сердце у астронавта бьется медленнее, чем у меня (также со скоростью 3/5 от моего), либо он сам сравнит ход светочасов со своим пульсом и заметит, что они идут медленнее, и таким образом сможет логически догадаться, что движется (а это противоречит первому постулату). Любые часы, имеющиеся у него на борту, также должны замедляться, идти со скоростью 3/5 от обычной, либо он сможет понять, что движется. Если у астронавта будет мюон (это нестабильная элементарная частица тяжелее электрона), который непременно распадается, то на борту ракеты он должен распадаться медленнее. Астронавт медленнее съедает обед. Еще… он… медленнее… разговаривает. Все процессы на борту ракеты идут медленнее.



