— Да, ты абсолютно прав. Если взять огромное число, а наше произведение состоит приблизительно из двух тысяч цифр, то разложить его на простые множители практически невозможно. Не существует эффективных алгоритмов для того, чтобы сделать это. Даже если мы знаем, что число представляет собой произведение двух простых чисел, то чтобы найти их, понадобится астрономическое число операций. И чем больше число, которое надо разложить на простые множители, тем больше операций нужно для этого, и количество операций растёт экспоненциально. А теперь ответьте мне: что в рассмотренном математическом формализме — замок, а что — ключ от него? Другими словами, чем мы будем шифровать, а чем расшифровывать?
Я задумался, а Катя ответила сразу же:
— Очевидно, произведение будет замком, то есть будет использоваться для шифрования. А вот его разложение на множители будет ключом — именно эту информацию надо хранить в тайне.
— Почему?
— Ну потому, что мы только что обсудили, что для того, чтобы получить произведение двух простых чисел, их надо просто перемножить. А для того чтобы разложить большое число на два простых, надо очень сильно постараться. Другими словами, то, что сделать просто, должно быть общедоступно. А вот то, что сделать практически невозможно, надо объявить тайной.
Отец сказал, что Катя полностью права. Затем он продолжил свои объяснения:
— На самом деле не всё так просто. В качестве открытых и закрытых ключей в алгоритме, про который я хочу вам рассказать, используются иные значения. Но они вычисляются на основе пары простых чисел. Давайте посмотрим…
Отец взял чистый лист бумаги и начал рисовать на нём алгоритм, поясняя его словами:
— Для начала надо выбрать два больших простых числа. Есть способы сделать это, чтобы не дать злоумышленнику легко взломать шифр, но мы сейчас не будем углубляться в детали. Если вы заинтересуетесь, то сможете узнать всё в специальной литературе. Как я уже сказал, выбранные числа должны быть очень большими. Но для пояснения алгоритма я буду использовать маленькие, чтобы можно было всё вычислить вручную.
Он записал на листке: 5 и 7. Затем он продолжил:
— Вторым шагом мы вычисляем произведение двух выбранных чисел. В нашем случае это будет 35. Но одновременно нужно дополнительно вычислить число, равное произведению двух выбранных чисел, из которых вычли по единице, то есть в нашем случае 4 и 6. Это будет 24, и оно является значением функции Эйлера для числа 35. Запомните это название. Возможно, в будущем оно вам понадобится.
Отец записал на листке: 5 Ч 7 = 35 и 4 Ч 6 = 24. Потом он продолжил:
— Третьим шагом мы должны выбрать так называемую открытую экспоненту. Это показатель степени, в которую будет возводиться сообщение при шифровании. Эта открытая экспонента должна быть взаимно простой с числом 24. Обычно выбирают какое-нибудь небольшое простое число, и есть специальные правила выбора, в которые мы углубляться не будем. Сейчас мы возьмём число 17. После выбора открытой экспоненты выполняется важный шаг — вычисление секретной экспоненты. Она вычисляется как обратная к открытой экспоненте по модулю 24. Другими словами, надо найти такое число, которое при умножении на 17 давало бы по модулю 24 значение 1. Это непростая задача. Помните ещё модульную арифметику?
Мы с Катей кивнули. Отец что-то посчитал на своём смартфоне и записал: e = 17, d = 41. Я спросил:
— Как тебе удалось так быстро найти обратное число?
— На самом деле я заранее подготовился, а сейчас просто проверил. Я же брал время для того, чтобы поразмыслить. Итак, продолжим. У нас получилось множество чисел, но использовать мы будем только три. В качестве открытого ключа используется пара (17, 35), а в качестве закрытого — пара (41, 35). Как видите, все не так, как рассказала Катерина. Но давайте посмотрим, почему этот способ тоже работает.
Нам надо выбрать сообщение, которое мы будем пересылать в шифрованном виде. Сообщения в этом методе — это целые числа от 1 до произведения двух выбранных простых чисел без единицы. Но вы же понимаете, что любой текст можно преобразовать в целое число. А если использовать очень большие простые числа, как я говорил вначале, то можно будет зашифровывать и большие тексты. Совсем большой текст можно разбивать на части и шифровать их друг за другом. Это уже дело техники. Итак, в нашем игрушечном примере нам надо выбрать сообщение в виде числа от 1 до 34. Катерина, выбери случайное число.
— Двадцать пять.
Отец продолжил писать на листке и комментировать:
— Хорошо. Для того чтобы зашифровать сообщение, мы должны возвести его в степень открытой экспоненты по модулю произведения двух простых чисел. В нашем случае мы должны взять число 25 и возвести его в степень 17 по модулю 35. Что получается? Так… Получается 30. Вот теперь это число 30 и есть наша шифровка. Как её расшифровать, кто-нибудь может предположить?
Мы с Катей только пожали плечами, а потому отец продолжил:
— Надо воспользоваться закрытым ключом. Шифровку надо возвести в степень закрытой экспоненты по тому же самому модулю. В нашем простом примере получается, что надо число 30 возвести в степень 41 по модулю 35. Получается… получается 25, как ни странно. Впрочем, почему должно быть странно? Ведь это методы шифрования и расшифровки.
Вроде бы всё было понятно. Мы с Катей некоторое время смотрели на написанные выкладки, а отец рисовал диаграмму алгоритма взаимодействия при шифровании этим методом. Теперь было ещё понятнее:
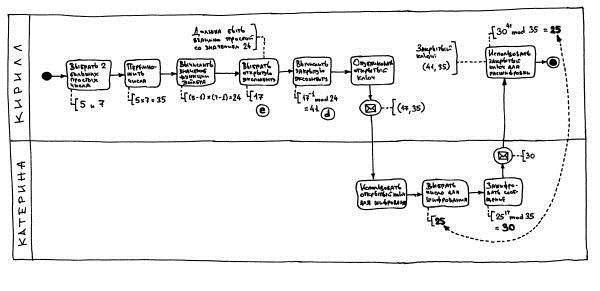
Ближе к вечеру вернулись мои дядьки. Дядя Руслан сразу же протянул нам пакет. Сердце у меня ёкнуло — мне показалось, что они нашли клад. Но, раскрыв пакет, я увидел только горсть всякого металлического добра. Дядя Руслан улыбнулся:
— Вот что удалось найти. Можете разобрать и взять себе, что найдёте интересным.
Мы с Катей накинулись на содержимое пакета. Оказалось, что дядя Руслан с дядей Игорем не только осматривали окрестности и пытались сопоставить план с местностью, но и прошлись с нашим металлоискателем по полям и тропинкам. Перед нашими глазами лежали: несколько болтов, какой-то крюк, дробинки и несколько монет. Я принёс чистую тряпочку, и мы тщательно, но осторожно оттерли с монет землю и грязь.
Насколько я мог судить, среди монет не было ни одной ценной: несколько советских монеток, а также одна дореволюционная — большая медная с надписью «1 копѣйка серебромъ». Мы с Катей не знали, как поступить, и я показал эту находку папе. Он сказал, что особой ценности эта монета не имеет, и я подарил её Кате на память.




