Что касается движения Солнца, то Птолемей удовольствовался теорией Гиппарха. Здесь он допустил огромный промах, поскольку в течение почти трехсот лет прецессия и смещение линии апсид (о чем он не знал) увеличили ошибку в 35′, сделанную Гиппархом, примерно до 5½°. Тропический год у Гиппарха оказался слишком долгим, следовательно, среднее движение – слишком малым, и ошибка за 300 лет (с 147 г. до н. э.) дошла до 76½′, к которым еще можно прибавить максимальную погрешность 22′ в уравнении центра из-за ошибки в значении эксцентриситета, из которого исходил Гиппарх.
Таким образом, ошибка в положении Солнца в таблицах Птолемея может составить около 100′. Поистине очень странно, что Птолемей никак не попытался улучшить точность солнечной теории; возможно, она недостаточно его интересовала по причине отсутствия каких-либо неравномерностей движения, кроме одного; но, разумеется, сложность измерения абсолютной долготы Солнца с любой степенью точности не могла не стать непреодолимым препятствием на пути к вычислению более точных числовых значений солнечной теории.
Но если мы обратимся к теории Луны, окажется, что Птолемей самым существенным образом усовершенствовал работу своего предшественника. Гиппарх лишь использовал эпицикл, движущийся на концентрическом с Землей деференте. Птолемей обнаружил, что нерешенные ошибки этой теории, уже смутно замеченные Гиппархом, достигают максимума в момент квадратуры и совершенно исчезают в сизигии; однако еще одна трудность заключалась в том, что ошибка не повторяется в каждой квадратуре, порой исчезая вовсе, а порой достигая целых 2°39′ – своего максимального значения. В конце концов выяснилось, что, когда Луна оказывалась в квадратуре и в то же время в перигее или апогее эпицикла, так что уравнение центра было равно нулю, местоположение Луны прекрасно согласовывалось с теорией Гиппарха, но при этом ошибка оказывалась наибольшей всякий раз, когда уравнение центра достигало максимума в момент квадратуры. Таким образом, действие второго неравенства всегда увеличивало абсолютное значение первого, особенно в квадратурах. Из этого следовал очевидный вывод, что радиус эпицикла имеет переменную длину, большую в квадратуре, чем в сизигии. Поскольку нельзя было предположить, что изменяется длина радиуса, изменяться должно было расстояние от поверхности Земли, чтобы она могла появляться под разными углами в разное время; другими словами, центр эпицикла должен был двигаться по эксцентру, но так, чтобы угловая скорость была равномерной, и не относительно центра круга, а относительно Земли.
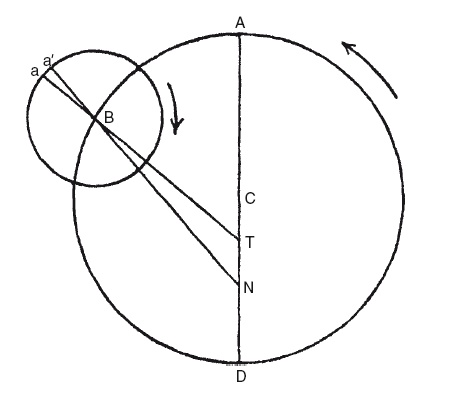
Но в то же время предполагается, что линия, проходящая через центр и апогей эксцентра, вращается в попятном направлении вокруг Земли, так что угол, который она образует с линией от Земли до центра эпицикла, угол АТВ, равнялся удвоенной элонгации Луны от Солнца, составляя 180° в первой и последней четверти
[172]. Таким образом, расстояние до В от Земли Т будет наибольшим в сизигии (фактически таким же, каким оно было бы по теории Гиппарха) и наименьшим в квадратуре. Второе неравенство происходит по причине того, что эпицикл не находится в том положении, в котором находился бы, если бы двигался по концентрическому кругу, и она равна углу между линиями, проведенными от Земли до двух местоположений Луны в соответствии с двумя теориями. Этот угол равен нулю в сизигии, так как центры эпицикла и эксцентра (В и С) находятся на одной линии с Землей и по одну сторону от нее, в то время как эпицикл лежит именно там, где должен находиться по теории Гиппарха. В квадратуре центры находятся на противоположных сторонах от Земли, и потому эпициклы, согласно двум теориям, наиболее удалены друг от друга. Если, однако, в это время Луна будет находиться в перигее или апогее эпицикла, он будет расположен на линии CD, а угол, представляющий второе неравенство, все равно будет равен нулю; в то время как наибольшего значения (2°39′) он достигнет, если линия, соединяющая Луну с В, будет находиться под прямым углом к этой линии, то есть когда аномалия Луны составит 90° или 270°. Исходя из максимального значения суммы двух неравенств 740′, с помощью простого вычисления получаем СТ: ТА = 49,7: 10,3.
Птолемей, таким образом, сделал большой шаг вперед, открыв второе неравенство, которое в наши дни называется эвекцией, и установив его величину – 1°19′30″, очень близкую к истинному значению, а также адаптировав к нему теорию Гиппарха. Однако продолжение наблюдений показало, что теория еще недостаточно разработана, так как в ней остаются нерешенные ошибки. Не смутившись этим, Птолемей снова приступил к решению проблемы, но не сумел обнаружить третье неравенство (вариацию) и лишь еще больше усложнил теорию. Аномалия, как мы видели выше, всегда отсчитывалась от линии апсид эпицикла, проходящей через Землю. Птолемей предположил, что она не проходит через Землю, но всегда направлена к точке N, расположенной на том же расстоянии от Г, что и С (ТС = TN). Среднее значение апогея, таким образом, составляет а′, в то время как видимый апогей а немного колеблется в обе стороны от положения среднего апогея, так что они совпадают в сизигиях и квадратурах. Поправку к аномалии, обусловленную таким расположением (просневсис, πρόσνευσις τοῦ ἐπικύκλου), следует применить к уравнению центра перед нахождением поправки на эвекцию.
По теории Птолемея, видимое местоположение Луны в момент сизигии и квадратуры можно определить с такой точностью, которая с практической точки зрения была достаточна для своего времени, поскольку он и его современники обладали лишь грубыми инструментами, неспособными фиксировать положение небесного тела без погрешности до 10′. Но хотя его теория таким образом оказалась почти достаточной для вычислений, она не позволяла определить фактическое местоположение Луны в пространстве, так как очень сильно преувеличивала вариацию расстояния от Луны до Земли. Опираясь на вавилонские наблюдения двух лунных затмений, происходивших вблизи апогея эпицикла, Птолемей находит видимый диаметр Луны в апогее эпицикла и эксцентра, равный 31°20″ (с превышением всего примерно на 2′). Из приведенных числовых данных нетрудно понять, что при наименьшем расстоянии от Земли диаметр Луны составит почти градус. Но хотя Птолемей не мог этого не заметить, он оставляет этот факт без внимания. Сейчас считается общепризнанным, что теория эпициклов была лишь средством для вычисления видимого положения планет и не претендовала на отображение истинной картины мира, и в этом смысле она, безусловно, достигла своей цели, причем в весьма элегантной манере с математической точки зрения. Для греческого ума теория обладала одним серьезным изъяном: в ней нарушался принцип строго равномерного движения как путем введения точки вне центра деферента, относительно которого угловое движение было равномерным, так и просневсисом. Это было совершенно непростительно с точки зрения физики, но математически, разумеется, вполне допустимо. Это был шаг к открытию эллиптического движения, но прошли многие века, прежде чем труд Птолемея был продолжен.



