
Глава 12.
ИНФЛЯЦИОННАЯ МОДЕЛЬ ВСЕЛЕННОЙ
Проблемы теории Большого взрыва
Из предыдущей главы мы узнали, как в 70-е годы XX века модель Большого взрыва подтвердилась практически с полной достоверностью. Однако в науке довольно часто бывает так, что модель, прекрасно согласующаяся со всеми данными и не имеющая видимой достойной альтернативы, все же сталкивается с некоторыми теоретическими или философскими проблемами. В конце концов, теория плоской Земли тоже когда-то согласовывалась со всеми данными наблюдений, доступными первобытным людям. А посмотрите только, как долго продержалась геоцентрическая модель Солнечной системы — не просто как миф, но как инструмент для точного предсказания движений планет. В 1980-х появляются рассмотренные далее теоретические проблемы, связанные с моделью Большого взрыва и признанные большинством космологов.
Проблема плоской Вселенной
Вспомним, что космологи выделяют параметр плотности Ω = ρ/ρc где ρ — средняя массовая плотность какого-либо компонента Вселенной, а ρc — критическая плотность, при которой Вселенная находится в точке равновесия между гравитационным коллапсом и бесконечным расширением. Если принять за ρc среднее значение плотности всех компонентов Вселенной, то Ω = 1 и Вселенная представляет собой плоскость, то есть в ней действует евклидова геометрия.
Но с этим есть одна проблема: согласно уравнениям Фридмана скорость расширения Вселенной определяется ее плотностью. Возьмем планковское время t = 10-43 с. Если бы в это время Ω была больше единицы хотя бы на 1/1060, Вселенная бы немедленно коллапсировала. Но при значении Ω меньше единицы хотя бы на 1/1060 Вселенная расширялась бы так быстро, что ее видимая часть вскоре стала бы настолько разреженной, что в ней не смогла бы появиться жизнь. В модели Большого взрыва жизнь может существовать только при Ω = 1, с огромной точностью, и Вселенная должна быть в высшей степени плоской.
Это как раз один из тех параметров, в отношении которых христианские апологеты заявляют, что Бог-творец должен был провести точную настройку, чтобы сделать существование жизни возможным
. В своей книге 2009 года «Жизнь после смерти: доказательства» (Life after Death: The Evidence)
. Динеш Д'Суза цитирует «Краткую историю времени» Стивена Хокинга: «Если бы через секунду после Большого взрыва скорость расширения оказалась хоть на одну сто квадрилионную (1/100 000 000 000 000 000) меньше, то произошло бы повторное сжатие Вселенной и она никогда бы не достигла своего современного состояния»
. УильямЛейн Крейг также ссылается на это утверждение в многочисленных дебатах
.
Проблема горизонта
Если исследовать небо в двух противоположных от Земли направлениях, мы увидим, что температура и спектр реликтового излучения одинаковы в обеих областях. Из этого следует, что РИ исходит из двух источников, которые на каком-то более раннем этапе были причинно связаны, благодаря чему смогли взаимодействовать друг с другом и установить тепловое равновесие. Две точки в пространстве могут быть причинно связаны, только если у них было достаточно времени, чтобы сигнал смог дойти от одной к другой и обратно. По последним данным, эти точки сейчас находятся на расстоянии 93 млрд. световых лет друг от друга.
В главе 10 мы выяснили, что фотоны реликтового излучения начали свое направленное движение, когда Вселенная стала прозрачной для них на 380 000-м году своей жизни. Если применить стандартную модель Большого взрыва с линейным расширением по закону Хаббла, выяснится, что расстояние между двумя точками по разные стороны Вселенной во время, когда ей было 380 000 лет, должно было составлять около 84 млн. световых лет, как показано на рис. 12.1. Это намного больше того расстояния, которое мог преодолеть свет от момента Большого взрыва, следовательно, источники A и B никогда не вступали в связь, которая бы позволила им установить тепловое равновесие.
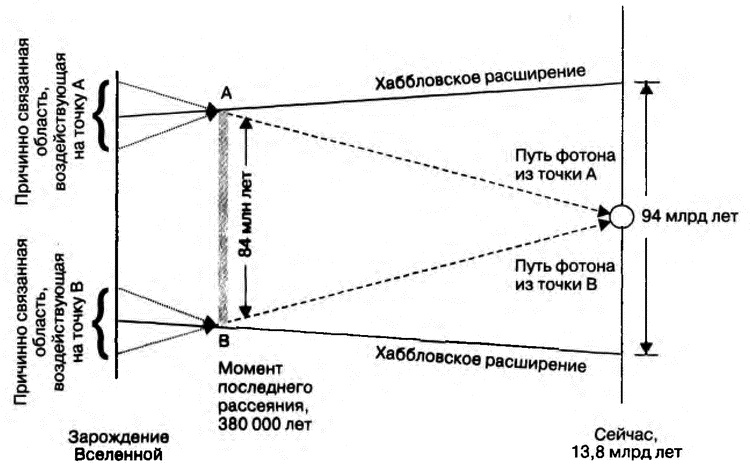
Рис. 12.1. Иллюстрация проблемы горизонта. Вдоль горизонтальной оси показано время, вдоль вертикальной — расстояние между двумя точками во Вселенной. Точки A и B на разных концах Вселенной в момент последнего рассеяния находились на расстоянии около 84 млн. световых лет друг от друга. Пути, проделанные фотонами, которые вышли из этих точек, показаны пунктирными линиями. В наши дни наблюдатели РИ регистрируют эти сигналы, идущие с двух противоположных направлений. Из-за расширения Вселенной сейчас они находятся на расстоянии 93 млрд. световых лет друг от друга. Коротким пунктиром обозначены световые лучи, показывающие, что области, которые могли воздействовать на точки A и B, никогда не были причинно связаны. Масштаб не соблюдается. Авторская иллюстрация
Проблема структуры
В главе 10 мы узнали, что космологи в течение многих лет силились объяснить, как в видимой Вселенной могли образоваться сложные структуры. Даже в рамках статической модели Вселенной это была довольно сложная проблема. В случае расширяющейся Вселенной все стало только хуже, ведь материя в ней рассеяна на большее расстояние, что делает еще менее вероятным гравитационный коллапс отдельных скоплений вещества.
Проблема монополей
В классической электромагнитной теории простейший электрический заряд представляет собой точечную частицу, электрическое поле которой можно показать наглядно в виде линий силы, расходящихся, как лучи, от центра. Два противоположных точечных заряда, положительный и отрицательный, формируют электрический диполь. Следовательно, отдельный точечный заряд можно назвать электрическим монополем. Существуют также квадруполи, октуполи и т. д. Если взять электрический диполь и растащить заряды в разные стороны, получатся два электрических монополя.
Магнитный брусок представляет собой пример магнитного диполя с северным и южным полюсами. Но если вы разделите магнитный диполь надвое, то не получите два магнитных монополя, вместо этого у вас появятся еще два диполя. В классической теории не существует магнитных монополей, и ни один до сих пор не удалось обнаружить экспериментально.
Как заметил в 1894 году французский физик Пьер Кюри, отсутствие магнитных монополей — это единственное различие между электричеством и магнетизмом. В 1931 году Поль Дирак доказал, что существование магнитных монополей согласуется с законами квантовой механики и тем самым восстанавливает электромагнитную симметрию
.
В 1974 году нидерландский физик Герард Хуфт
и советский физик Александр Поляков
независимо друг от друга доказали, что в рамках калибровочных теорий объединения, включающих электромагнитное взаимодействие, должны существовать магнитные монополи. В 1976 году британский физик Томас Киббл (один из шести авторов, предложивших в 1964 году механизм Хиггса, см. главу 11) доказал, что при фазовом переходе с нарушением калибровочной симметрии новая фаза не обязана быть однородной, но может иметь так называемые топологические дефекты, подобные тем, которые возникают в ферромагнетиках. Эти дефекты включают доменные стенки, струны и монополи
.

