Даже если бы у нас была квантовая теория гравитации, похоже, что у нас не было бы возможности проверить ее предсказания в планковском состоянии, в котором она предположительно применима. Тем не менее квантовая гравитация вполне может иметь измеримые эффекты. Например, на расстояниях, близких к планковским, пространство-время должно быть «бугристым», то есть вместо гладкого континуума мы должны увидеть знаменитую квантовую пену, предложенную Джоном Уилером в 1955 году
.
Как ни удивительно, оказывается, что эта пенистость, в принципе, обнаружима. Вспомните пассаж о гамма-всплесках в главе 13. Они происходят в далеких галактиках, на расстоянии миллиардов световых лет, и излучают фотоны высоких энергий. Считается, что это происходит в результате столкновения двух нейтронных звезд. Эти фотоны могут взаимодействовать с квантовой пеной и задерживаться на пути к Земле. Данный эффект можно наблюдать, если измерить время прибытия двух или более фотонов, которые были испущены одновременно в одном всплеске.
Используя данные о гамма-всплесках, полученные космическим гамма-телескопом Ферми, астроном Роберт Немирофф и его соавторы сравнили время прибытия гамма-фотонов разных энергий, излученных из одного источника. В случае гамма-всплеска GRB 090510, зарегистрированного в мае 2009 года на расстоянии 7 млрд. световых лет от нас, прибытие трех фотонов было зафиксировано в пределах 1 мс
. Этот результат накладывает ограничения на размер пузырьков пространственно-временной пены — в 525 раз меньше планковской длины. Хотя результат требует независимого подтверждения, похоже, что пространство-время в наблюдаемой Вселенной гладко.
Может возникнуть вопрос, как это значение согласуется с утверждением, которое я высказал в главе 6, что никакое расстояние меньше планковской длины нельзя измерить. Ответ имеет отношение к разнице между теорией и экспериментом, которую я раз за разом подчеркиваю в этой книге. Реально было измерено вовсе не расстояние короче планковской длины. Тем не менее измеренное значение было включено в теоретическую модель, в результате предсказавшую ограничение на размер пузырьков, которые должны быть значительно меньше планковской длины. Но само это число существует только в рамках модели, а не в прямом наблюдении.
Бивселенная
Теперь давайте поставим вопрос, что могло существовать по отрицательную сторону нашей временной оси, то есть до t = О в нашем прошлом. Откуда же взялась эта первичная сфера абсолютного хаоса? Хотя у нас нет никакой эмпирической информации о том, что могло происходить до планковского времени, мы все еще можем применить наши наиболее глубокие теоретические знания, то есть общую теорию относительности и квантовую теорию, которые были основаны на эмпирических свидетельствах из более позднего времени.
В книге и статье 2006 года я описал сценарий, который обосновывает естественное происхождение нашей Вселенной и вытекает из общепризнанной физики и космологии
. Он строится на модели, предложенной в 1982 году Дэвидом Аткацем и Хайнцем Пейджелсом
. Я выработал этот сценарий чисто математически на уровне, доступном для студента-физика, в значительной степени полагаясь на очень приятное учебное пособие, опубликованное Аткацем в 1994 году, «Квантовая космология для пешеходов»
. Здесь я только кратко опишу порядок действий.
В 1982 году Аткац и Пейджелс показали, каким образом наша Вселенная могла появиться благодаря квантовому туннелированию. Этот механизм был предложен Виленкиным в 1982 году
, а также Джеймсом Хартлом и Стивеном Хокингом в 1983 году
.
Начнем с уравнений Фридмана для пустой, гомогенной, изотропной Вселенной с положительной кривизной, то есть с параметром кривизны k = +1. Хотя наша Вселенная очень близка к плоской, из этого не обязательно следует, что глобальный параметр кривизны k = 0; она может иметь k = +1 или k = -1 и все еще быть очень, очень плоской после инфляции. Аткац и Пейджелс показали, что туннелирование работает только при k = +1.
Имея в распоряжении это уравнение, мы следуем стандартным правилам, согласно которым нужно перейти от классического уравнения к квантово-механическому, заменив действительные числа математическими операторами
[25]. Результат выглядит неожиданно просто. Вы получаете квантово-механическое, не зависящее от времени уравнение Шрёдингера для нерелятивистской частицы с массой, равной половине планковскои массы, и нулевой полной энергией, которое имеет единственное измерение, представляющее собой космологический масштабный коэффициент Вселенной, который мы можем принять за радиус Вселенной. Следует отметить, что это просто математическое тождество и из него не следует, что такая частица существует.
Выведенное уравнение — это упрощенная форма уравнения Уилера — Девитта, решение которого гордо именуется волновой функцией Вселенной
. При стандартном квантово-механическом подходе к интерпретации волновых функций квадрат амплитуды волновой функции Вселенной определяет вероятность нахождения конкретной Вселенной среди ансамбля похожих вселенных.
Итоговый сценарий проиллюстрирован схемой пространства-времени на рис. 15.2. Время t изображено вертикально, а два из трех измерений пространства, x и y, показаны в перспективе. В каждый момент времени расширяющаяся сферическая Вселенная спроецирована на окружность, перпендикулярную временной оси. Она развивается из сферы планковских размеров, расположенной в начальной точке, t=0.
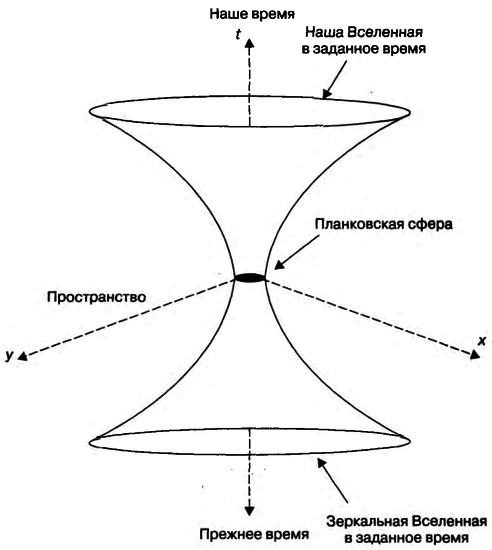
Рис. 15.2. Схема пространства-времени, изображающая нашу Вселенную и зеркальную Вселенную, которые развиваются из одной планковской сферы в противоположных временных направлениях. Одно пространственное измерение скрыто, поэтому сферические вселенные и планковская сфера спроецированы на окружности. Авторская иллюстрация
Также показана зеркальная Вселенная на противоположной стороне временной оси. Если мы посмотрим на уравнения Фридмана и другие космологические уравнения, то увидим: ничего в них не запрещает отрицательное время. Зеркальная Вселенная развивается из той же планковскои сферы в противоположном временном направлении. Заметьте, что это не противоречит картине временных линий, изображенной на рис. 15.1.
А вот следствие, которое редко отмечают: поскольку зеркальная Вселенная существует в нашем прошлом, ее стрела времени направлена противоположно нашей. Как мы узнали из главы 5, в физических уравнениях не используется направление времени. Привычная, обиходная стрела времени — это исключительно статистическое определение, в котором будущее время — это направление наиболее вероятных событий, в соответствии с ростом энтропии нашей Вселенной
. Таким образом, поскольку зеркальная Вселенная расширяется в противоположную сторону от нашей, направление стрелы времени, которое было бы определено наблюдателем в этой вселенной, противоположно нашему.



