Как показывается в серии доскональных исследований Эрика Ван Нимвегена
[43], различные функциональные классы генов по-разному соотносятся с общим числом генов в геноме (Molina and van Nimwegen, 2009; van Nimwegen, 2003). Не учитывая некоторые отклонения, для прокариот можно указать три основных показателя степени, описывающие эти соотношения: 0, 1 и 2. Генам белков, участвующих в информационных процессах (трансляции, транскрипции и репликации), соответствует показатель степени 0 — число таких генов достигает некоторого константного значения уже в минимальных геномах и в принципе не зависит от сложности генома. Число метаболических ферментов и транспортных белков примерно прямо пропорционально общему числу генов (показатель степени 1). Регуляторные гены и компоненты систем передачи сигналов показывают квадратичную зависимость (показатель степени равен 2; рис. 4-10). Показатели степени этих трех обширных классов остаются неизменными, с очень небольшими отклонениями, для всех групп прокариот, и это позволяет предположить, что разница в эволюционной динамике генов с различными функциями отражает какие-то фундаментальные законы эволюции клеточных организмов, или, другими словами, строгие и четко выраженные ограничения в функциональном устройстве геномов. Для генов эукариот обнаружены похожие, хотя и не такие явные, степенные соотношения, показатель степени для регуляторных генов эукариот значительно больше 1 (хотя и меньше 2). Имея в виду все вышесказанное, можно заключить, что эти соотношения представляют еще один набор универсалий геномной эволюции, которые становятся еще интереснее при рассмотрении их связи с функциональным устройством клетки.
Фундаментальные причины существования различных соотношений для различных функциональных классов генов еще не выяснены. Привлекательно простая модель эволюции метаболических сетей прокариот как «ящика с инструментами», предложенная Сергеем Масловым и коллегами, может быть первым шагом на пути объяснения квадратичной зависимости, характерной для регуляторных генов (Maslov et al., 2009). В этой модели ферменты, необходимые для утилизации новых метаболитов, добавляются вместе с соответствующими им регуляторами (в первую очередь посредством горизонтального переноса генов, гл. 5) во все более развитую сеть реакций. В результате усложнения сети, обеспечивающей все большее разнообразие ферментов промежуточных реакций, увеличивается отношение числа регуляторных генов к регулируемым. В какой-то момент, и его наступление можно точно предсказать, цена добавления новых регуляторов неизбежно станет слишком невыгодной («разрастающаяся бюрократия») и будет ограничивать рост сложности генома.
Гипотеза «бюрократического потолка» для верхней границы сложности генома выглядит особенно правдоподобно в свете почти полного отсутствия роста числа генов в геномах позвоночных, особенно млекопитающих (и в наших геномах тоже), для которых связь между числом генов и размером генома очевидно нарушена (см. гл. 3 и 8). В принципе число генов могло бы быть напрямую ограничено ценой репликации ДНК, но для огромных геномов позвоночных этот фактор можно смело исключить как главное ограничение. Соответственно, цена регуляции, возможно совместно с ценой экспрессии, выглядит наиболее вероятным кандидатом на роль основного фактора, ограничивающего рост числа генов. Поэтому не случайно позвоночные (и в меньшей степени другие многоклеточные эукариоты) выработали новые, замысловатые способы увеличения сложности протеома, такие как широко распространенный альтернативный сплайсинг, альтернативная трансляция и сложная регуляция (в особенности обширный, все еще слабо изученный набор регуляторных РНК). Такие формы сложности не вызывают инфляционный рост числа белок-кодирующих генов и, таким образом, снижают по крайней мере некоторые издержки, особенно издержки трансляции (см. гл. 8).
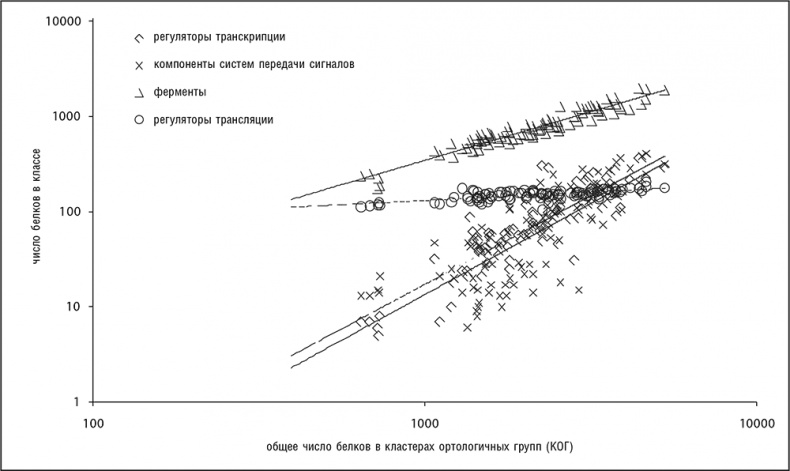
Рис. 4-10. Четко различающиеся соотношения между различными функциональными классами генов и размером генома (общим числом белок-кодирующих генов) прокариот. Использована информация из базы данных COG (Tatusov et al., 2003). График построен в двойных логарифмических координатах.
Универсальная зависимость численности функциональных классов генов от размера генома находится в обратной зависимости с ранее описанным степенным законом распределения численности семейств генов. Чем больше положительный показатель степени функции зависимости от размера генома для функционального класса генов (рис. 4-10), тем меньше отрицательный показатель степени функции распределения численности семейств в этом классе (рис. 4-7). Кажется интуитивно правдоподобным, что функциональные классы с сильной зависимостью от размера генома должны содержать много больших семейств паралогичных генов. Обратная зависимость этих двух универсалий генома была выведена в рамках простой эволюционной модели, в которой используются правила пропорциональных вычислений для функциональной композиции генома, например «добавить два регулятора на каждый метаболический фермент» (Grilli et al., 2011). Предсказания этой модели подтверждаются эмпирическими данными для многих геномов бактерий и архей.
Стохастичность, нейтральность и отбор в эволюции
В предыдущих разделах этой главы мы ознакомились со многими количественными универсалиями, отражающими важнейшие аспекты эволюции и функционирования генома. Среди этих универсалий мы рассматривали вездесущий степенной закон распределения, который описывает как структуру всех биологических сетей, так и семейства паралогичных генов в разнообразных геномах, близкое к логарифмически нормальному распределение скоростей эволюции генов и универсальные корреляции, такие как отрицательная корреляция между генной экспрессией и скоростью эволюции. Какова природа этих универсалий? Отражают ли они какие-то глубокие свойства эволюции или это просто статистические эффекты, не имеющие отношения к пониманию биологических явлений? Здесь и далее в этой книге (гл. 13) будет отстаиваться точка зрения на эти универсалии как на нетривиальные, характерные и биологически значимые тенденции, хотя они отражают только одну из двух (а возможно, и большего числа) дополнительных (в смысле принципа дополнительности Бора) составляющих эволюции жизни
[44].



