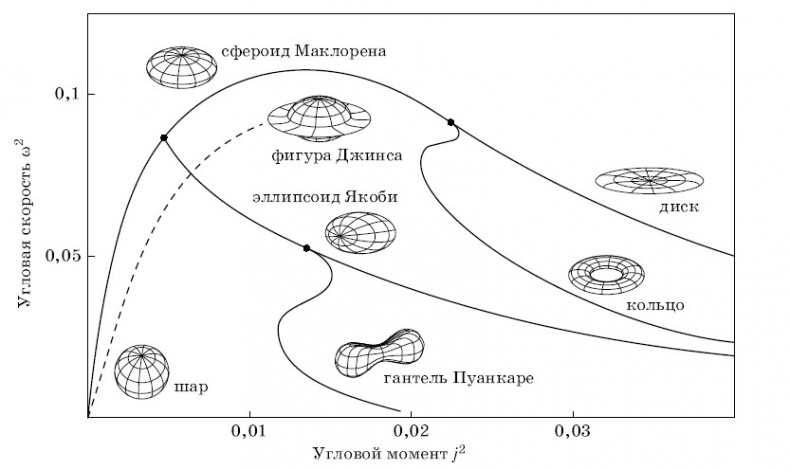
Рис.7. Формы вращающихся тел. Указаны последовательности фигур равновесия несжимаемых, «жидких» тел (сплошные линии) и сжимаемых, газовых тел (пунктир). Оси вращения у всех фигур на рисунке расположены вертикально.
Небесные тела лунных и более размеров резко неоднородны: плотность в центре существенно превышает плотность у поверхности. Для Земли — на порядок, для Юпитера — на 4-5 порядков, для Солнца — на 7 порядков. Так что однородные фигуры равновесия служат лишь крайне упрощенными моделями. Но в случае медленного вращения форму поверхности можно представить аналогичным (7) рядом Ляпунова:
ƒ(φ)= R[ƒ0(φ)+ƒ1(φ)+ƒ2(φ) +…] (8)
Тут требуются пояснения. Форму поверхности вращения естественно задавать уравнением r=ƒ(φ), связывающим широту φ с расстоянием от поверхности до центра масс r функциональной зависимостью ƒ. Таков смысл левой части (8). В правой части R — характерный размер тела, например, радиус равновеликого шара. Тогда ƒ0 тождественно равна единице, так что в нулевом приближении тело является шаром r=R — const. Остальные члены ряда дают малые поправки, причем ƒs пропорциональна qs. Здесь q=ω2R3/(GM) представляет собой безразмерный малый параметр, равный отношению центробежной силы к силе тяготения на экваторе шара массы М и радиуса R. Для Земли, Юпитера, Солнца q равно соответственно 0,0034; 0,083; 0,00002. Наибольшим значением q=0,139 в Солнечной системе обладает Сатурн.
Функция ƒ1 имеет вид ƒ1(φ)= Aq(1—3sin2φ), где число А определяется распределением масс внутри тела Т. Для однородного тела А=5/12. Для противоположного крайнего случая сосредоточенной в центре массы, окруженной невесомой атмосферой, А=1/6. Остальные ƒs можно найти последовательно методом Ляпунова.
Функция ƒ, представляющая поверхность сжатого эллипсоида вращения Е, также может быть разложена в ряд (8), причем ƒ0=1. ƒ1=е2(1—3sin2(φ))/6, где е — эксцентриситет меридионального сечения. Подбирая его так, чтобы Aq=е2/6, добьемся совпадения Rƒ0 и Rƒ1 у Т и Е. Таким образом, любая фигура равновесия в нулевом приближении — шар, в первом — сжатый эллипсоид вращения.
Движение ИСЗ
Как рассчитывают трассы небесных тел в сложных гравитационных полях? Простых формул, подобных выведенным Кеплером и Ньютоном для описания движения частицы вокруг шара, для сложных полей не существует. Более того, за редчайшими исключениями вообще не существует абсолютно точных формул. Это следствие реальной сложности движений. Какими же средствами располагает современная наука? В самых общих чертах их можно разделить на две группы.
1. Аналитические методы. С их помощью сложное движение можно представить как наложение бесконечного числа простых движений. До предела упрощенный пример — знакомая по школьным учебникам формула суммы бесконечного числа членов геометрической прогрессии
1/x=1+(1-x)+(1-x)2+(1-x)3+… (9)
Предположим, что марсиане умеют складывать, вычитать и умножать числа, представленные десятичными дробями, и знают, что есть и обратное умножению действие — деление, но делить не научились. Так вот, левую часть (9) марсиане смогут вычислить, складывая большое количество чисел из правой части, а каждое из них получается умножением (1—х) самого на себя. Уже на этом простейшем примере видны две особенности аналитического подхода.
Во-первых, для получения точного ответа нужно проделать бесконечно много операций, что невозможно. Но для достижения заданной точности нужно произвести уже конечное число операций. Последнее тем больше, чем выше требования к точности. Пусть, например, х=1,1. Чтобы ошибка (9) составила не больше 0,01, следует взять два слагаемых справа; четыре слагаемых гарантируют погрешность менее 0,0001.
Во-вторых, формулы аналитического метода работают не для одного какого-то набора значений переменных величин, а для любых их значений из некоторой области. Так, равенство (9) можно применять не только при х=1,1, а для всех значений х от нуля до двух. Но для х=—1,5 формула (9) не годится и приходится прибегать к другим соотношениям. Напимер, для —2<х<0 можно применить формулу 1/х=—[1+(1+х)+(1+х)2+(1+х)3+…]. В небесной механике орбиты разного типа также описываются разным набором аналитических формул.
2. Численные методы представляют собой вычисление положения и скорости частицы в последовательные моменты, разделенные небольшими промежутками времени, по соответствующим значениям этих величин и действующих сил в предшествующие моменты. Такой путь прост и универсален. Большое количество вычислений в век электроники — недостаток не самый важный. Хуже, что получается лишь одна траектория и даже для соседней все вычисления приходится выполнять с самого начала.
На практике нередко комбинируют аналитический и численный методы, что привело к впечатляющим успехам в описании движения планет, их спутников, комет, астероидов. Но мы нарушим исторический порядок, обратившись сначала к искусственным небесным телам. ИСЗ ближе к нам и двигаются сравнительно просто. Естественно переходить от простого к сложному.
Свой виток вокруг планеты спутник проходит почти точно по эллипсу, но виток не замкнется. Следующий оборот будет отличаться от предыдущего примерно на 1/300, так как настолько притяжение Земли вблизи ее поверхности отличается от притяжения шара. За триста оборотов (примерно месяц для близких ИСЗ) орбита может измениться до неузнаваемости. Меняется не все. Истинное движение мало (в пределах 10км) отклоняется от движения по некоторому опорному эллипсу. Опорный эллипс имеет фиксированные размер, форму и наклон к плоскости экватора, но вращается вокруг двух осей одновременно. Во-первых, линия апсид (соединяющая перигей и апогей) поворачивается в плоскости эллипса с угловой скоростью ω1. Во-вторых, сама эта плоскость поворачивается вокруг полярной оси с угловой скоростью ω2. В терминах небесной механики перицентр испытывает вековое возмущение со скоростью ω1 а восходящий узел орбиты на экваторе — вековое возмущение со скоростью ω2. В результате траектория типичного ИСЗ приобретает вид запутанного клубка, изображенного на рис.8. Описанные свойства надо учитывать при проектировании, чтобы спутник с успехом выполнял свою работу.
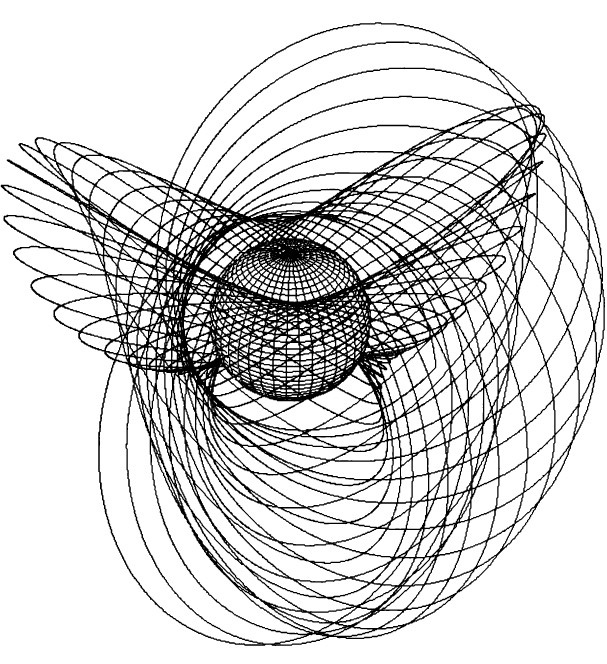
Рис.8




