Теперь, когда все эти и другие проверки были выполнены с большой тщательностью и точностью, доводы в пользу здравомыслия непоколебимы.
Чтобы завершить это обсуждение, мы должны отметить еще два факта однородности физических законов, помимо однородности во времени, которые почти в той же мере являются основополагающими в устройстве мира: однородность в пространстве и однородность вещества. Однородность в пространстве, которую мы упоминали ранее, проверяется в тех же лабораторных и астрономических тестах, что и однородность во времени. Кроме того, вдохновленные Нётер, мы можем проверить ее иначе – проверяя сохранение импульса! Опять же это ни в коем случае не попытка позолотить лилию, потому что сохранение импульса проходит тщательную проверку в анализе реакций элементарных, где исследуются очень экстремальные условия.
Наконец, есть однородность вещества – тот наблюдаемый факт, что у всех электронов (например) абсолютно одинаковые свойства. Это допущение неявно подразумевается в любом приложении современной атомной физики, электроники и химии. Хотя оно часто считается само собой разумеющимся, это абсолютно неочевидно.
В человеческом производстве использование взаимозаменяемых частей было революционным новшеством, достижение которого потребовало тяжелого труда. Тем не менее задолго до новшеств Сэмьюела Кольта и Генри Форда Творец Природы предвидел достоинства взаимозаменяемых частей. В сегодняшней Главной теории взаимозаменяемость электронов следует из того факта, что все электроны (например) являются минимальными возбуждениями – квантами – вездесущего, заполняющего мир электронного флюида, и того, что свойства этого флюида однородны в пространстве и времени. Таким образом, в рамках квантовой теории однородность вещества не требует отдельных допущений. Она вытекает из однородности пространства и времени, а следовательно, как нас учила Эмми Нётер, из симметрии.
Квантовая красота IV: Доверяем красоте
Притча о додекаэдре
Додекаэдр уже появлялся несколько раз в нашей медитации. Будучи одним из пяти платоновых тел, он воплощает немало геометрической симметрии. Согласно самому Платону, это форма Вселенной в целом. Мы видели, как Сальвадор Дали использовал символизм додекаэдра, чтобы выразить космическое соединение, которое могло бы быть трудно перенести на холст иначе. Мы также нашли додекаэдр, скрывающийся в пределах каждого из бесконечного разнообразия фуллеренов, где его 12 пятиугольников обеспечивают шестиугольникам графена возможность образовать замкнутую поверхность.
У додекаэдров также есть одно очень практичное применение: в качестве настольного календаря. Они прекрасно подходят для этого, поскольку имеют 12 граней, совершенно одинаковых, так что вы можете поместить по месяцу на каждой. В Интернете легко можно найти инструкции, как сделать такие календари, вырезав их из жесткой бумаги или картона.
Додекаэдр – красивая вещь, и к настоящему времени он стал нам близким другом.
Теперь предположим, что некий игривый дух хочет проверить наш характер или дать нам радость решения милой головоломки. Он разъединяет части схемы и убирает метки, и мы получаем загадку, изображенную на илл. 39.
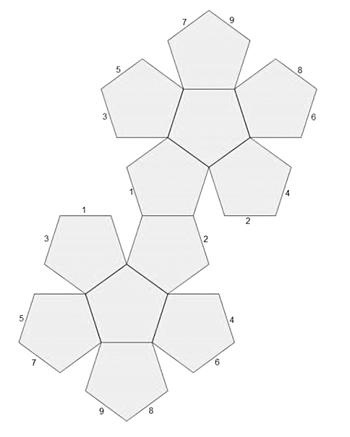
Илл. 38. Этот красивый чертеж позволит вам сделать додекаэдр. Для этого нужно начертить такую схему на жесткой бумаге или картоне, затем вырезать по границам и согнуть вдоль внутренних сплошных линий так, чтобы одинаково обозначенные стороны оказались вместе
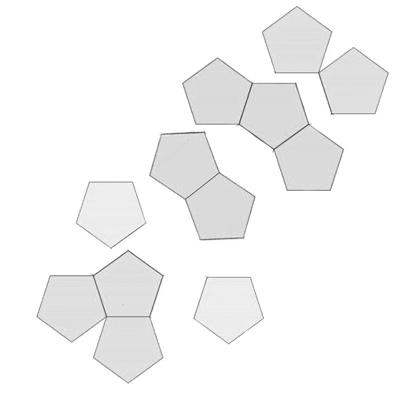
Илл. 39. С разделенной на части схемой изображение становится более трудным для интерпретации, но очевидные намеки на его происхождение остаются. Знакомство с додекаэдром приведет нас от этого набора кусочков обратно к илл. 38 и оттуда к нашему платонову додекаэдру
Здесь труднее понять, что мы видим. Большинство людей, которые в последнее время, возможно, не очень-то думали о додекаэдрах, не знало бы, что сделать с этой неполной схемой. Но те из нас, кто медитировал о красоте и ее воплощениях, подготовлены к этому испытанию. Двенадцать идентичных, правильных пятиугольников, у некоторых пар общая сторона, некоторые тройки готовы образовать вершины – это сразу наводит на мысль! Мы распознаем скрытый потенциал чертежа и готовы сделать из него что-то красивое.
Помня об этом триумфе, давайте теперь возвратимся к нашей Главной теории. Она описывает огромное изобилие фактов – точных количественных наблюдений о физическом мире – с помощью очень небольшого набора уравнений. Она является, как мы уже обсуждали, более чем достаточной основой для химии, инженерного дела, биологии (вероятно), астрофизики и большей части космологии. К тому же она изящна. У уравнений Главной теории есть глубокие корни в симметрии. Поэтому мы можем восстановить всю Главную теорию из нескольких общих правил о том, к каким пространствам свойств имеют доступ различные частицы, и указаний о том, какой (локальной) симметрией должны обладать эти пространства. Мы можем указать необходимые данные на достаточно простых резюмирующих иллюстрациях (см. вклейки TT и UU).
Главная теория замечательно описывает Природу. Было бы трудно преувеличить ее точность, ее мощь или ее красоту. И все же ценители предельной красоты не будут удовлетворены. Именно потому, что она так близка к окончательному описанию Природы, мы должны поддерживать Главную теорию на максимально возможном уровне эстетических стандартов. Если тщательно исследовать ее в таком критическом духе, Главная теория обнаруживает недостатки.
• Она содержит три математически похожих взаимодействия: сильное, слабое и электромагнитное. Все они являются воплощением общего принципа: локальной симметрии пространств свойств. И гравитация – это четвертое взаимодействие. Она также основана на локальной симметрии, хотя и другого рода: локальной галилеевой симметрии. Гравитация также является намного более слабой, чем другие взаимодействия. Было бы убедительнее и красивее иметь одну основную симметрию и одно всеобщее взаимодействие, которые бы давали согласованное описание Природы. Три (или четыре) определенно больше одного, следовательно, мы еще не пришли к цели.
• Что еще хуже, даже после того, как мы установили частицы, которые «на самом деле» являются одной и той же сущностью, по-разному расположенной в своем пространстве, мы оказываемся с шестью не связанными между собой «фундаментальными» объектами. Шесть также определенно больше одного.
• У нас также есть утроение семейств, которое представляется бессмысленным.
• У нас также есть флюид Хиггса, который играет уникальную и важную роль в теории, но пока выглядит еще одной независимой движущейся частью. Флюид Хиггса был введен, чтобы залатать дыры (что он и делает), а не для красоты (и он ее не добавляет).

