Что экспериментаторы делают в действительности, чтобы исследовать поведение на маленьких расстояниях, так это стреляют частицами друг по другу и изучают вероятность отклонения на (относительно) большие углы. Затем мы восстанавливаем картину, реконструируя по отклонениям частиц те силы, которые их вызывали. Вы можете вспомнить, что именно такой была стратегия, которую Резерфорд, Гейгер и Марсден использовали для изучения внутреннего строения атомов около 1912 г. Основной принцип не изменился, но сегодня, сталкивая частицы с гораздо большей энергией, мы получаем доступ к более коротким расстояниям.
Сравнение других взаимодействий с гравитацией несколько хитрее. С одной стороны, насколько нам известно, нет никакой фундаментальной «единицы заряда» для гравитации – она реагирует на энергию. С другой стороны, мы используем пробные объекты, которые имеют различную энергию, чтобы сравнивать взаимодействия на различных расстояниях. Поэтому при оценке относительной силы гравитации на этих расстояниях мы просто подставляем в уравнения энергию, соответствующую этому расстоянию, и вычисляем гравитационную силу, с которой она действует. Конец технического отступления.)
Переосмысление асимптотической свободы
Однако, зайдя так далеко, мы не должны сдаваться так легко. И действительно, еще один большой урок Главной теории – асимптотическая свобода – подсказывает решение. В предыдущей главе мы видели, насколько важно для понимания сильного взаимодействия осознавать, что сила этого взаимодействия меняется в зависимости от расстояния – становясь более интенсивной на больших расстояниях и менее ощутимой на коротких. Такая изменчивость свойств позволила нам увязать конфайнмент кварков, который указывает на мощную силу, препятствующую их большому удалению друг от друга, с их независимостью, которая указывает на незначительную силу на маленьких расстояниях.
Асимптотическая свобода ведет нас в правильном направлении. Поскольку интенсивность сильного взаимодействия становится слабее на более коротких расстояниях, различие между ним и другими взаимодействиями уменьшается.
Возможно ли, что они все объединятся?
Чтобы перейти от надежды к концепции, а затем от нее к расчету, будет полезно заново продумать асимптотическую свободу, используя образы и понятия, которые применяются в общей практике – отвлеченно от сильного взаимодействия и даже от Главной теории.
Давайте посмотрим на все более живыми и проницательными глазами.
Цветная вклейка XX показывает, что бы мы увидели, глядя на «пустое место», если бы наши глаза могли разрешить временные интервалы порядка 10−24 секунды и объекты или размеры порядка 10–14 см.
Эта иллюстрация, если быть точнее, представляет собой мгновенный снимок типичного распределения плотности энергии, являющейся результатом флуктуаций интенсивности глюонного поля. Флуктуации такого рода возникают самопроизвольно в любой точке пространства и в любой момент времени, будучи следствиями квантовой механики. (О них иногда говорят как о виртуальных частицах или нулевых колебаниях.) Спонтанная активность глюонного флюида ответственна за асимптотическую свободу, конфайнмент и за большую часть нашей с вами массы, как мы уже обсуждали. Поскольку они выступают как центральное звено в расчетах, которые были проверены на соответствие действительности очень точно и разными способами, существование этих колебаний является настолько бесспорным, насколько это может быть в науке. На этой «вычисленной» иллюстрации самые большие концентрации энергии обозначены «самыми горячими» цветами – красным и ярко-желтым, в то время как менее интенсивным участкам соответствуют бледно-желтый, зеленый и, наконец, голубой. Области, где плотность энергии ниже пороговой, оставлены без цвета на черном фоне. Увеличение этого изображения приблизительно 1027, так что отображаемая область, грубо говоря, столь же мала по сравнению с человеком, как человек мал по сравнению с видимой Вселенной. Приблизительно через 10−24 секунды картина флуктуаций меняется. Это время гораздо меньше по сравнению с секундой, чем секунда – по сравнению со временем, прошедшим после Большого взрыва.
Поскольку КХД была проверена с почти невероятной строгостью, можно с величайшей степенью определенности, возможной в науке, сказать, что эта картина точно изображает то, что происходило, происходит и будет происходить все время и повсюду.
Более того! Глюонный флюид ни в коем случае не является единственным квантовым флюидом. Мы также подтверждаем расчетом, что фотонный (электромагнитный) флюид флуктуирует и что флюиды виконов тоже флуктуируют. И то же происходит с флюидами, связанными с рождением и исчезновением частиц «вещества» – кварков и лептонов. Электронный флюид флуктуирует, флюид верхнего кварка флуктуирует и т. д. Физические последствия флуктуаций в этих других флюидах обычно меньше, чем эффект флуктуаций в глюонных флюидах, потому что глюонов много (их восемь!) и они сильно взаимодействуют. Но общие принципы квантовой теории предсказывают флуктуации во всех квантовых флюидах, и есть многочисленные и надежные доказательства на базе точных измерений, что эти флуктуации имеют место. Чтобы откорректировать наш взгляд, мы должны принять их все во внимание.
Так же, как вода вносит искажения в то, как рыбы видят свой мир, так и среда пространства – в частности, активность квантовых флюидов, которые его заполняют, – искажает наше восприятие самых маленьких расстояний. Чтобы воспринять лежащие в основе фундаментальные принципы, мы должны сделать поправку на эти искажения. И в этом наша надежда. Различные взаимодействия кажутся неравными по интенсивности. Но возможно, как только мы исправим наше зрение, они окажутся равными.
Почти попали
Вот что происходит, если выполнить эту программу (илл. 40). Как вы можете видеть, она почти работает – три линии, представляющие интенсивности различных взаимодействий, почти сходятся в одной точке. Но не совсем.
Я хочу дать некоторую дополнительную информацию об илл. 40 на случай, если вам захочется понять ее во всех деталях. Чтобы представить результат в настолько простом виде, насколько это возможно, – три прямых линии! – мне пришлось сделать два не самых обычных шага, которые обозначены в подписях к осям. Я сделал так, что по вертикали отложены обратные интенсивности, так что чем выше интенсивность взаимодействия, тем ниже точка на графике. (Этот, на первый взгляд, странный выбор имеет еще одно важное преимущество, которое проявится на илл. 41.) На горизонтальной же оси я использовал логарифмическую шкалу. Таким образом, каждый шаг вправо уменьшает расстояние и увеличивает энергию, которая нам нужна, чтобы получить доступ к таким расстояниям, в 10 раз! Следовательно, наш расчет, несмотря на его скромный вид, возносит нас далеко вверх от энергий, которых в настоящий момент достигают ускорители. Толщина линий обозначает их экспериментальную и теоретическую неопределенности.
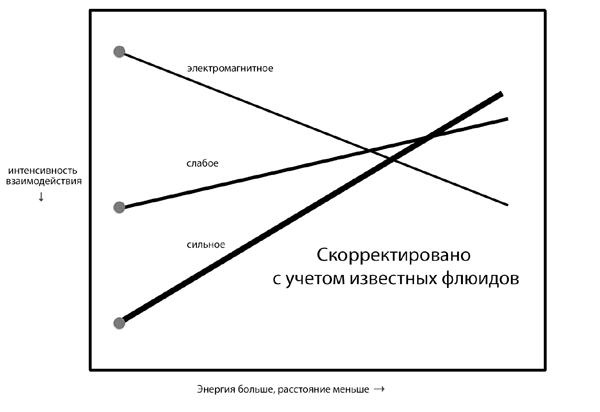
Илл. 40. Как только внесены поправки на влияние известных квантовых флюидов, мы находим, что объединение почти имеет место и остается лишь незначительное отклонение

