Наконец, Ньютон переходит к доказательствам из астрономии в Книге III, которая называется «Система мира». В то время, когда вышло первое издание «Математических начал», существовало всеобщее согласие по поводу правильности Первого закона Кеплера, то есть эллиптической формы орбит планет, но все еще оставались некоторые сомнения по поводу Второго и Третьего законов о том, что радиус-вектор от Солнца до планеты описывает равные площади за равные промежутки времени, и о том, что квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей их орбит. Кажется, Ньютон зацепился за законы Кеплера не потому, что они были хорошо сформулированы, а потому что подходили к его собственной теории. В Книге III он отмечает, что спутники Юпитера и Сатурна ведут себя соответственно Второму и Третьему законам Кеплера, что наблюдаемые фазы пяти планет (кроме Земли) доказывают, что они обращаются вокруг Солнца, что все шесть планет подчиняются законам Кеплера и что Луна удовлетворяет Второму закону Кеплера
{264}. Его собственные тщательные наблюдения кометы 1680 г. показывают, что она тоже движется по коническому сечению: по эллипсу или гиперболе, в любом случае – очень близко к параболе. Из всего этого (и своих более ранних сравнений центростремительного ускорения Луны и ускорения свободного падения тел около поверхности Земли) Ньютон заключил, что существует центральная сила, подчиняющаяся закону обратных квадратов, которая притягивает спутники Юпитера, Сатурна и Земли к планетам, а также все планеты и кометы – к Солнцу. Из того факта, что ускорение производится силой тяжести независимо от природы тела, которое ускоряется, будь это планета, спутник или яблоко, и зависит только от природы тела, производящего силу, и расстояния между ними, а также учитывая тот факт, что ускорение, производимое любой силой, обратно пропорционально массе тела, на которое оно воздействует, Ньютон пришел к выводу, что сила тяготения, действующая на любое тело, должна быть пропорциональна массе тела, что отменяет зависимость от массы тела при расчетах ускорения. Это создает четкое различие между силой тяготения и магнетизмом, который по-разному действует на тела с разным составом, даже когда они имеют одинаковую массу.
Далее в Предложении 7 Ньютон использовал свой Третий закон движения, чтобы определить, как сила притяжения зависит от природы тела, ее производящего. Рассматривая два тела, 1 и 2, с массами m1 и m2, Ньютон показал, что сила притяжения, оказывающая влияние со стороны тела 1 на тело 2, пропорциональна m2, а сила, оказывающая влияние со стороны тела 2 на тело 1, пропорциональна m1. Но в соответствии с Третьим законом эти силы равны по модулю, поэтому каждая из них должна быть пропорциональна m1 и m2.. Ньютон мог проверить Третий закон в случаях столкновения тел, но не при гравитационных взаимодействиях. Как подчеркивал Джордж Смит, только много лет спустя стало возможно подтвердить пропорциональность силы притяжения инертной массе как притягивающего, так и притягиваемого тела. Тем не менее Ньютон пришел к заключению, что «тяготение существует во всех телах повсеместно, и оно пропорционально количеству материи в каждом из них». Именно поэтому произведения центростремительного ускорения различных планет на квадрат их расстояния до Солнца намного больше, чем произведение центростремительного ускорения Луны на квадрат ее расстояния до Земли: все дело в том, что Солнце, которое притягивает планеты, намного массивнее, чем Земля.
Эти результаты Ньютона обычно представляют в виде формулы для силы притяжения F между двумя телами с массами m1 и m2, разделенными расстоянием r:
где G – это универсальная постоянная, сегодня известная как постоянная Ньютона, или гравитационная постоянная. Ни эта формула, ни постоянная G не появляются в «Математических началах». Даже если бы Ньютон ввел эту постоянную, он не смог бы определить ее значение, потому что не знал массу Солнца и Земли. В расчетах движения Луны или планет G появляется только как множитель для массы, соответственно, Земли или Солнца.
Даже не зная значения G, Ньютон смог использовать свою теорию притяжения, чтобы рассчитать соотношения масс различных тел в Солнечной системе (см. техническое замечание 35). Например, зная отношения расстояний от Юпитера и Сатурна до их спутников и до Солнца и зная отношения орбитальных периодов Юпитера и Сатурна и их спутников, он смог высчитать отношения центростремительных ускорений для спутников Юпитера и Сатурна в направлении их центральных планет к центростремительным ускорениям самих этих планет в направлении к Солнцу. Из этого Ньютон смог вывести соотношение масс Юпитера, Сатурна и Солнца. Поскольку у Земли также есть спутник, ту же самую технику можно в принципе использовать, чтобы высчитать соотношение масс Земли и Солнца. К сожалению, несмотря на то что расстояние между Землей и Луной было хорошо известно благодаря суточному параллаксу Луны, суточный параллакс Солнца был слишком мал, чтобы его измерить, таким образом соотношение расстояний между Землей и Солнцем и Землей и Луной не было известно (как мы уже видели в главе 7, информация, полученная Аристархом, и расстояния, которые он высчитал, пользуясь ею, были безнадежно неточны). Тем не менее Ньютон пошел дальше и рассчитал соотношения масс, используя значение расстояния от Земли до Солнца, которое было, скорее, нижней границей этой величины и составляло примерно половину настоящего значения. В таблице приводятся вычисленные Ньютоном соотношения масс, приведенные в качестве следствия из Теоремы VIII Книги III «Математических начал», в сравнении с современными значениями
{265}.
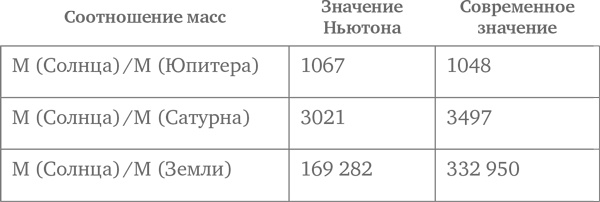
Как видно из этой таблицы, полученный Ньютоном результат для Юпитера совпадает с истинным значением очень хорошо, для Сатурна – неплохо, но для Земли – очень отличается, потому что расстояние от Земли до Солнца не было известно. Ньютон был вполне осведомлен о проблемах, которые возникают по причине неточности в наблюдениях, но, как и большинство ученых до начала XX в., был достаточно небрежен по поводу точности в результатах своих расчетов. К тому же Ньютон, как и его предшественники Аристарх и аль-Бируни, приводил эти результаты с гораздо большим количеством значащих цифр, чем это позволяла точность данных, на которых были основаны расчеты.



