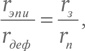13. Эпициклы внутренних и внешних планет
В своем «Альмагесте» Птолемей представил теорию движения планет, согласно которой, в ее простейшем виде, каждая планета движется по окружности, называемой эпициклом, вокруг точки в пространстве, которая сама обращается вокруг Земли по окружности, которая называется деферент. Здесь мы ответим на вопрос, почему эта теория работала так хорошо, предсказывая видимые движения планет. Ответ на него оказывается различным для случая внутренних планет (Меркурия и Венеры) и внешних планет (Марса, Юпитера и Сатурна).
Сначала рассмотрим внутренние планеты – Меркурий и Венеру. По современным представлениям, и Земля, и эти планеты обращаются вокруг Солнца на приблизительно постоянном расстоянии от него и примерно с неизменной скоростью. Если мы не станем принимать во внимание законы физики, мы можем считать, что в центре находится Земля. Тогда Солнце будет обращаться вокруг нее, а все остальные планеты будут обращаться вокруг Солнца на постоянных расстояниях и с постоянными скоростями. Это представление соответствует простейшему варианту теории, позднее предложенной Тихо Браге, сторонником которой, возможно, был и Гераклид. Она дает верные предсказания положений планет, не считая небольших поправок, необходимых потому, что планеты на самом деле движутся по эллиптическим орбитам, близким к круговым, а не в точности по окружностям, и Солнце расположено не в центрах этих эллипсов, а на некотором расстоянии от центров, к тому же и скорость планеты слегка изменяется по мере ее движения по орбите. Описанная система является особым случаем планетной теории Птолемея, хотя сам Птолемей такой случай никогда не рассматривал: в нем деферентом является не что иное, как орбита Солнца вокруг Земли, а эпициклом – орбита Меркурия или Венеры вокруг Солнца.
Заботясь лишь о расчете видимых положений Солнца и планет, переменное расстояние любой планеты от Земли можно умножать на произвольную константу, получая тот же самый результат. Так получится, например, если радиус и эпицикла, и деферента планеты помножить на одно и то же число, которое для Меркурия и Венеры может быть произвольно различным. Допустим, мы примем, что радиус деферента Венеры равен половине расстояния от Земли до Солнца, а радиус ее эпицикла – половине радиуса орбиты Венеры вокруг Солнца. Это не скажется на том факте, что центры эпициклов планет все время будут располагаться на прямой, проходящей через Землю и Солнце (см. рис. 7а, на котором схематично, не в истинном масштабе, изображен пример эпицикла и деферента внутренней планеты). Эта трансформация не скажется на видимом движении Венеры и Меркурия по небу до тех пор, пока мы не поменяем соотношение радиусов эпицикла и деферента каждой из планет. Такова упрощенная версия теории, предложенной Птолемеем для описания движений внутренних планет. Согласно ей, один оборот планеты по эпициклу занимает столько же времени, сколько ей в реальности необходимо для оборота вокруг Солнца: 88 суток для Меркурия и 225 суток для Венеры. При этом центр эпицикла, как и Солнце, обращается вокруг Земли, и один его полный оборот занимает промежуток времени, равный земному году.
Предметно говоря, притом что мы не меняем отношения радиусов эпицикла и деферента, должно быть справедливо равенство
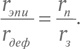
Здесь rэпи и rдеф – радиусы эпицикла и деферента в системе Птолемея, а rп и rз – радиусы орбит той же планеты и Земли в системе Коперника (или, что то же самое, радиус орбит планеты вокруг Солнца и Солнца вокруг Земли, соответственно, в теории Тихо Браге). Конечно, Птолемей ничего не знал о системах Тихо Браге или Коперника, и свою теорию он разрабатывал иным путем. Все сказанное по этому поводу выше лишь показывает, почему теория Птолемея работала, а не то, каким образом он вывел ее.
Теперь обратимся к внешним планетам – Марсу, Юпитеру и Сатурну. В простейшей версии теории Коперника (как и у Тихо Браге) каждая из этих планет постоянно находится на одном и том же расстоянии не только от Солнца, но и от точки C’, движущейся в пространстве, сохраняя одно и то же расстояние от Земли. Чтобы найти эту точку, начертим параллелограмм (рис. 7б), первые три вершины которого в порядке против часовой стрелки будут таковы: S – точка расположения Солнца, E – точка расположения Земли, P’ – точка расположения одной из планет. Движущаяся точка C’ находится в четвертом, пустом углу этого параллелограмма.
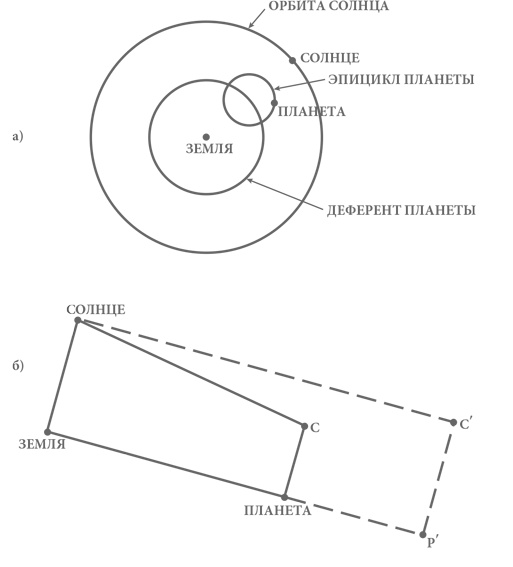
Рис. 7. Упрощенная версия теории эпициклов, описанной Птолемеем: а) схема, согласно Птолемею, изображающая движение одной из внутренних планет – Меркурия или Венеры; б) схема движения одной из внешних планет – Марса, Юпитера или Сатурна – согласно теории Птолемея. Планета P обращается по эпициклу вокруг точки C за один год, при этом отрезок CP всегда параллелен отрезку, соединяющему Землю и Солнце, в то время как сама точка C обращается вокруг Земли по деференту за более длительное время (штриховые линии отражают особый случай теории Птолемея, в котором она эквивалентна теории Коперника).
Поскольку отрезок ES имеет фиксированную длину, а отрезок P’C’ является противоположной ему стороной параллелограмма, то P’C’ также имеет фиксированную длину, равную длине первого отрезка. Поэтому планета все время остается на одном и том же расстоянии от C’, равном расстоянию от Земли до Солнца. Это особый случай теории Птолемея, не рассмотренный им самим. В нем деферент – не что иное, как орбита точки C’ вокруг Земли, а эпицикл – орбита Марса, Юпитера или Сатурна вокруг точки С’.
И вновь, если думать лишь о расчете видимых положений Солнца и планет, можно умножить переменное расстояние любой планеты от Земли на произвольную константу, не меняя видимую картину, и этого можно достигнуть, перемножая радиусы эпицикла и деферента каждой планеты на одну и ту же постоянную величину, индивидуальную для каждой внешней планеты. И хотя у нас больше не получается параллелограмм, отрезок от планеты до точки C остается параллельным отрезку между Солнцем и Землей. Видимое движение любой из внешних планет по небу не изменится в результате такой трансформации, если неизменным останется соотношение радиусов ее деферента и эпицикла. Такова упрощенная версия теории Птолемея, предложенной им для описания движения внешних планет. Согласно ей, один оборот по эпициклу вокруг точки C планета совершает за год, в то время как точка C обращается по деференту вокруг Земли за то время, которое по-настоящему требуется планете, чтобы совершить оборот по орбите вокруг Солнца: 1,9 земных лет для Марса, 12 лет для Юпитера, 29 лет для Сатурна.
При неизменности отношения радиусов деферента и эпицикла должно быть справедливо равенство