
Онлайн книга «Объясняя мир. Истоки современной науки»
где rэпи и rдеф снова обозначают радиусы эпицикла и деферента в системе Птолемея, а rп и rз – радиусы орбит планеты и Земли, соответственно, в системе Коперника (или, аналогично, радиус орбиты планеты вокруг Солнца и радиус орбиты Солнца вокруг Земли в системе Тихо Браге). Опять же, здесь мы не описали то, каким образом Птолемей пришел к формулировкам своей теории, а лишь пояснили причину того, почему она работала довольно хорошо.
Обозначим угол между направлением в зенит и на Луну, видимую из некоторой точки O земной поверхности, как ζ’ (дзета штрих). Луна непрерывно и равномерно движется вокруг центра Земли, поэтому, анализируя серию повторяющихся наблюдений Луны, можно вычислить направление от центра Земли C к центру Луны M. В частности, можно рассчитать угол ζ между лучом, на котором находится отрезок CM, и лучом из центра Земли C, пересекающим поверхность Земли в точке O, который совпадает с направлением в зенит в этой точке. Углы ζ и ζ’ слегка отличаются, потому что радиус Земли rз, хотя и мал по сравнению с расстоянием между центром Земли и Луной d, но не пренебрежимо мал. Именно из разности этих углов Птолемей смог вывести отношение d/rз.
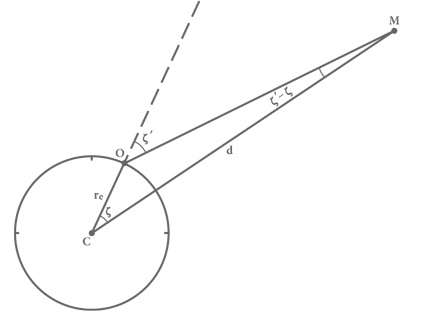
Рис. 8. Использование параллакса для определения расстояния до Луны. Здесь ζ’ – угол между наблюдаемым положением Луны и вертикалью, а ζ – то значение, которое было бы у этого угла, если можно было наблюдать Луну из центра Земли.
Точки C, O и M образуют треугольник, в котором угол при вершине C равен ζ, угол при вершине O равен 180° – ζ’, а при вершине M, поскольку сумма углов любого треугольника равна 180°, угол будет 180° − ζ – (180° − ζ’) = ζ’ − ζ (см. рис. 8). Отношение d/rз из значений этих углов мы можем получить намного проще, чем это делал Птолемей, воспользовавшись теоремой из современной тригонометрии: в любом треугольнике длина каждой стороны пропорциональна синусу противолежащего угла (о том, что такое синус, расскажем в техническом замечании 15). Угол, противолежащий отрезку CO длиной rз, равен ζ’ − ζ, а угол, противолежащий отрезку CM длиной d, равен 180° − ζ, поэтому
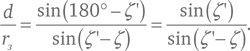
1 октября 135 г. Птолемей определил, что зенитный угол при наблюдении из Александрии составляет ζ’ = 50°55’, и его расчеты показали, что в тот же самый момент при наблюдении из центра Земли угол ζ был бы равен 49°48’. Соответствующие синусы этих углов равны
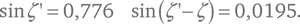
Зная эти числа, Птолемей смог заключить, что расстояние от центра Земли до Луны в единицах радиуса Земли составляет:
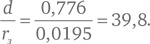
Эта величина существенно меньше, чем настоящее значение, в среднем примерно равное 60. Проблема оказалась в том, что Птолемей неточно определил разность углов ζ’ и ζ, но по крайней мере полученный результат давал верное представление о том, какого порядка величина расстояния до Луны.
Так или иначе, Птолемей рассчитал его более точно, чем Аристарх, который на основании своих расчетов отношения диаметров Земли и Луны, а также расстояния до Луны к ее диаметру смог бы указать предельные значения для d/rз, равные 215/9 = 23,9 и 57/4 = 14,3. Однако если бы Аристарх использовал правильное значение 1/2° для углового диаметра лунного диска вместо неверной величины 2°, то соотношение d/rз у него получилось бы в 4 раза больше, в промежутке от 57,2 до 95,6. Такой промежуток включал бы истинную величину.
Раздел современной математики, который называется тригонометрией, изучаемый сейчас в школах и высших учебных заведениях, мог бы здорово помочь античным математикам и астрономам. Тригонометрия учит, каким образом, зная любой из углов прямоугольного треугольника, кроме прямого, вычислить соотношения всех его сторон. Например, результат деления длины катета, противолежащего данному углу, на длину гипотенузы является значением функции под названием «синус угла». Это число можно найти в математических таблицах или рассчитать на калькуляторе, если ввести значение угла и нажать кнопку «sin». В том же треугольнике отношение прилежащего к тому же углу катета к гипотенузе называется косинусом угла, а противолежащего катета к прилежащему – его же тангенсом, но нам сейчас достаточно поговорить о синусах. Хотя синус ни разу не упоминается в трудах математиков эпохи эллинизма, в «Альмагесте» Птолемея встречается связанная с ним функция, которая называется хордой угла.
Чтобы дать определение хорде угла θ (тета), нарисуем окружность радиусом 1 (в любых удобных для вас единицах измерения длины) и проведем из ее центра два луча, разделенные углом θ. Хордой угла будет в этом случае называться отрезок, соединяющий точки пересечения этих двух радиусов с окружностью (см. рис. 9). В «Алмагесте» приводится таблица хорд [30] в вавилонской шестидесятеричной системе счисления, в которой углы выражены в градусах, в промежутке от 1/2° до 180°. Например, для угла 45° в таблице дано значение хорды 45 55 19, что можно перевести в привычный нам вид таким образом:
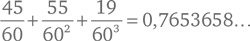
В то же время истинное значение равняется 0,7653669…
Хорды естественным образом применяются в астрономии. Если мы представим себе, что звезды расположены на сфере единичного радиуса, центр которой совпадает с центром Земли, то, если две звезды разделены угловым расстоянием θ, воображаемый отрезок, соединяющий эти две звезды на сфере по прямой, будет иметь длину хорды угла θ.
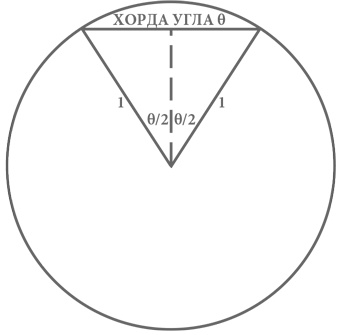
Рис. 9. Хорда угла θ. Начерченная здесь окружность имеет радиус, равный 1. Два изображенных сплошной линией радиуса образуют угол θ. Горизонтальный отрезок проведен между точками пересечения радиусов с окружностью. Его длина равна хорде этого угла.
