18. Эллипсы
Эллипсом называется определенный вид замкнутой кривой на плоскости. Есть как минимум три различных способа дать определения этой кривой.
Определение первое
Эллипс – это множество точек на плоскости, координаты которых удовлетворяют уравнению:
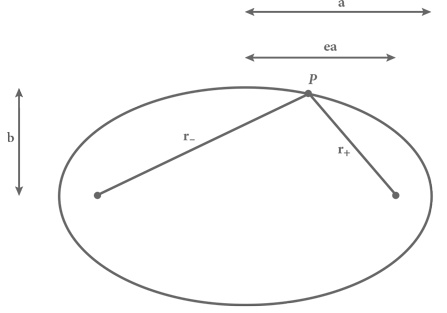
Рис. 12. Элементы эллипса. Две точки, обозначенные внутри эллипса, называются его фокусами; a и b – большая и малая полуоси эллипса; расстояние от любого из фокусов до его центра равно ea. Сумма длин отрезков r+ и r−, соединяющих оба фокуса с произвольной точкой P на линии эллипса, постоянна и равна 2a. У изображенного здесь эллипса эксцентриситет e ≈ 0,8.

где x – расстояние от центра эллипса до любой точки на его линии вдоль одной оси координат, а y – расстояние до той же самой точки вдоль оси, перпендикулярной первой. a и b – положительные коэффициенты, характеризующие размер и форму эллипса, которые принято выбирать так, что a ≥ b. Для ясности можно считать, что x – горизонтальная, а y – вертикальная ось координат, хотя, разумеется, они могут быть расположены вдоль любых двух взаимно перпендикулярных направлений. Из уравнения (1) следует, что расстояние r = √(x² + y²) до любой точки на линии эллипса от его центра, расположенного в координатах x = 0, y = 0, удовлетворяет условиям
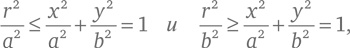
поэтому для любой точки эллипса справедливо:
Обратим внимание, что в точках пересечения горизонтальной оси y = 0, поэтому x² = a², и, значит, x = ±a. Таким образом, уравнение (1) описывает эллипс, наиболее длинный диаметр которого простирается от −a до +a в горизонтальном направлении. Также в точках, где эллипс пересекает вертикальную ось, выполняется x = 0, поэтому y² = b², и, значит, y = ±b, а, следовательно, уравнение (1) описывает эллипс, наиболее короткий диаметр расположен вертикально от −b до +b (см. рис. 12). Параметр a называется большой полуосью эллипса. Принято выражать другой параметр эллипса, его эксцентриситет, как

В общем случае эксцентриситет находится в пределах от 0 до 1. Эллипс с эксцентриситетом e = 0 есть окружность с радиусом a = b. Эллипс с эксцентриситетом e = 1 сплюснут настолько, что является просто отрезком горизонтальной оси с вертикальной координатой y = 0.
Определение второе
Другое классическое определение эллипса таково, что это множество точек на плоскости, для которых сумма расстояний до двух фиксированных точек (фокусов эллипса) постоянна. Для эллипса, описываемого уравнением (1), эти две точки расположены в координатах х = ±ea, y = 0, где e – эксцентриситет, определяемый тождеством (3). Пара расстояний от этих двух точек до произвольной точки на линии эллипса, координаты x и y которой удовлетворяют уравнению (1), выражается таким образом:
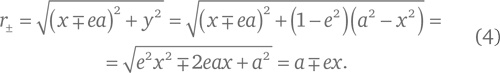
Так что их сумма действительно является постоянной величиной:

Это можно рассматривать как обобщение классического определения окружности как множества точек, отстоящих на постоянное расстояние от фиксированной точки.
Поскольку оба фокуса эллипса полностью симметричны, средние расстояния r+ и r− до точек на эллипсе (при равном весе усреднения для любого сегмента заданной длины, взятого на линии эллипса) от двух фокусов должны быть равны: r+ = r−, и значит, из равенства (5) получаем:
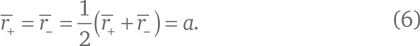
Это же число является средним между самым большим и самым малым расстоянием от точек на эллипсе до любого из фокусов:
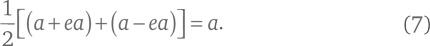
Определение третье
Данное Аполлонием Пергским исходное определение эллипса таково: это коническое сечение, которое получается, если рассечь конус плоскостью, наклоненной к оси конуса. Выражаясь современным математическим языком, конус с ориентированной вертикально осью – это трехмерное множество точек, удовлетворяющее такому условию: радиусы круговых поперечных сечений конуса пропорциональны расстоянию, отложенному по вертикали:

где u и y – расстояния, отложенные вдоль двух взаимно перпендикулярных горизонтальных направлений, z – расстояние вдоль вертикальной оси, а α – положительный коэффициент, определяющий форму конуса (по какой причине мы обозначили первую горизонтальную координату u, а не x, вы скоро поймете). Вершиной этого конуса является точка, в которой u = y = 0, а также z = 0. Плоскость, которая рассекает конус под углом, можно определить как множество точек, удовлетворяющих следующему равенству:

где β и γ – еще два коэффициента, которые определяют, соответственно, угол наклона и высоту расположения плоскости (координаты мы определяем таким образом, что плоскость оказывается параллельной оси y). Совмещая равенства (8) и (9), получаем:

