«Ясно, что орбита планеты не круглая; она сжимается по бокам и снова расширяется до амплитуды круга в перигее. Такая форма называется овалом»
[187].
Находился ли Кеплер, сознательно или бессознательно, под влиянием гипотезы Тихо Браге о том, что кометы могут двигаться по овальным орбитам? Или, как и Тихо Браге, он пришел к такому заключению на основании аналогичных свидетельств?
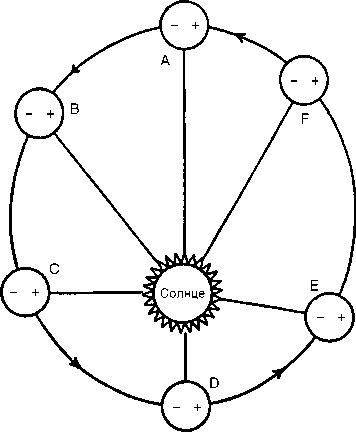
Рис. 10. Кеплеровское объяснение эллиптической орбиты с использованием магнитных сил. Когда планета вращается вокруг Солнца против часовой стрелки, его два магнитных полюса сохраняют одинаковую ориентацию по отношению к орбите. В точках А и D, равноудаленных от Солнца, планета не имеет тенденции ни к приближению, ни к удалению от него. Когда планета движется от А к D (как в В и С), притягивающий полюс находится ближе к Солнцу, а планета поэтому стремится приблизиться к нему; когда она движется от D к А (как в Е и F), отталкивающий полюс ближе к Солнцу, и планета стремится удалиться от него. Отсюда эллипс
Как обычно, Кеплер не удовлетворился теоретическими рассуждениями – ему было необходимо найти физический смысл. В этом случае, считал он, отклонение от круга может объясняться результатом влияния магнитной силы Солнца, которая изменяется в зависимости от расстояния и является самой сильной в перигее (когда планета ближе всего к Солнцу). Магнитная сила воздействует на планету, вращающуюся по кругу под влиянием своего собственного движущего средства, и в результате получается овоид (яйцевидная фигура).
Овоид оказался весьма упрямой кривой. После множества бесплодных попыток Кеплер воскликнул: «Ах, если бы наша фигура была эллипсом! Ее можно было бы описать с помощью метода Архимеда»
[188]. Но все оказалось не так просто, и он продолжал упорно трудиться, стараясь рассчитать овоид, принимая каждый его край за идеальный эллипс. Но только расчеты, проведенные им таким образом для Марса, не согласовывались с наблюдениями. Не важно, какую комбинацию эллипсов он использовал для максимального приближения к овоиду, – проблема казалась нерешаемой. Наконец, после нескольких лет бесплодных попыток Кеплер решил, что все дело в конкретном овоиде, который у него получился. Вероятно, фигура ошибочна, и надо испробовать другую, пусть даже это означает, что все расчеты надо начинать заново. Первый же эллипс, который он испытал, продемонстрировал числовое соответствие, которое, казалось, оправдало использование эллипса; но только и на этот раз Кеплер потерпел поражение, теперь из-за арифметической ошибки. Впору было прийти в отчаяние.
До сих пор Кеплер использовал эллипсы как инструменты для аппроксимации. Неожиданно ему пришло в голову, что, если (как и должно быть, согласно его теории «магнетизма») Марс колеблется на диаметре эпицикла, двигаясь вокруг Солнца («классическая» концепция), кривая в результате будет именно эллипсом. Удивленный собственной глупостью, не позволившей ему сразу увидеть, что и физические идеи, и используемая геометрия подталкивали к одному неизбежному выводу, Кеплер вернулся к расчетам и сразу нашел ошибку в арифметике, не позволившую ему достичь успеха раньше. В качестве еще одной награды он обнаружил, что в действительности не может быть никакой другой кривой, кроме эллипса (с Солнцем в одном фокусе), которая бы соответствовала имеющейся информации и одновременно согласовывалась с законом площадей
[189].
Удивление Кеплера и его предыдущее отрицание эллипса как возможной орбиты, а не инструмента для вычислений не является таким невероятным, как может показаться на первый взгляд. Конические сечения в XVI веке были еще плохо изучены. Сам Кеплер жаловался: «Много ли математиков одолели «Конические сечения» Аполлония Пергского?»
[190] Только спустя восемьдесят лет Ньютон посоветует будущему читателю его «Математических начал натуральной философии» (Principia) ознакомиться с трудом Аполлония для лучшего понимания астрономической теории. Даже Кеплер, чрезвычайно довольный своим решением, не был уверен, что понял физический смысл эллипса так же уверенно, как физический смысл эксцентрической окружности, поскольку слишком много элементов было чисто геометрическими. Действительно, в одном фокусе было Солнце, но другой был пуст, как и центр. Однако наблюдения и вычисления не могут лгать, и Кеплер похвастался:
«Путем трудоемких демонстраций, выполнив множество расчетов, я открыл, что путь планеты в небесах – это не круг, а овал – совершенной формы эллипс»
[191].
Кеплер рассчитал новые орбиты всех планет, включая Землю, и обнаружил, что они все эллиптические, хотя, как правило, имеют значительно меньший эксцентриситет, чем орбита Марса.
Нерешенной осталась одна проблема: что определяет относительные размеры планетарных орбит? Этому Кеплер посвятил Mysterium Cosmographicum. Спустя четверть века Кеплер вернулся к изучению связи скоростей движения планет на разных частях орбит, промежутков времени, необходимых разным планетам для прохождения орбит, и средних расстояний до Солнца. Он был уверен, что должны существовать интересные и важные математические отношения между скоростями и расстояниями, которые, в свою очередь, имеют физическое толкование. И конечно, эти отношения, когда будут найдены, подтвердят и прольют свет на божественную гармонию и размеры Вселенной.
Все более поздние исследования этого предмета Кеплером содержатся в «Пяти книгах о гармонии мира», где он по привычке скрупулезно перечислил все свои медленные и мучительные шаги к двум определенным принципам и напомнил читателям о своих предыдущих открытиях. Первая книга почти целиком посвящена геометрии, в частности гармоничным пропорциям плоских фигур, не имеющим никакого отношения к астрономии. Вторая книга тоже по большей части является геометрической (Кеплер назвал ее архитектурной), только в ней рассматриваются твердые тела. Третья книга – пифагорейское исследование гармонии; она объясняет математические пропорции, ответственные за музыкальную гармонию. В четвертой книге, наконец, появляется физический мир. Это «метафизическая, психологическая и астрологическая» книга о душах и телах в небесах и на земле.
И только пятая – «астрономическая и метафизическая» – книга посвящена предмету, который так долго занимал Кеплера: гармонии небесных движений, основанной на математике и метафизике предыдущей книги. Здесь имеется краткое повторение основной доктрины Mysterium Cosmographicum в связи с системами Коперника и Тихо Браге. Но есть в ней и новая доктрина: в третьей главе Кеплер представляет «краткое изложение астрономических доктрин, необходимое для размышлений о гармонии небес», которое на самом деле является кратким описанием его новейшего открытия. Автор вспоминал долгие недели труда, ушедшего на рассмотрение отношений между движениями планет и размером их орбит. Он не сразу увидел истину, но наконец его осенило, и он смог говорить о своих выводах с полной уверенностью: квадраты периодов обращения планет вокруг Солнца относятся как кубы полуосей орбит планет. Кеплер понимал, что его выводы важны, но все же не мог осознать насколько. Он, естественно, видел метафизическую важность своего закона лучше, чем физическую, и это вдохновило его на новые вычисления. Он сравнил пропорции между разными элементами планетарных орбит, составил таблицы гармоний, которые затем сравнил с численными пропорциями разных нот октавы или с геометрическими пропорциями длин струн, испускающих разные ноты. Сравнив астрономические, цифровые и геометрические пропорции, он создал то, что назвал «музыкой сфер». Таким образом, Кеплер решил древнюю пифагорейскую задачу и показал гармонию мира.



