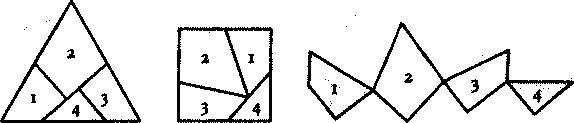
Головоломка галантерейщика
* * *
Юный канадец Эрик Демейн был одним из тех, на кого «Головоломка галантерейщика» произвела неизгладимое впечатление. Он рос вункеркиндом, и к 20 годам уже стал профессором Массачусетского технологического института. Особенно Демейна заинтересовала «универсальность» проблемы. Он задался вопросом, возможно ли всякую фигуру с прямолинейными сторонами разбить на части, а затем шарнирно соединить эти части друг с другом так, чтобы они сворачивались в любую другую заданную фигуру той же площади с прямолинейными сторонами. Он посвятил работе над этой задачей десять лет и в марте 2008 года (в возрасте 27 лет) объявил о полученном решении перед очень восприимчивой аудиторией — в бальном зале одной из гостиниц в Атланте, где он делал доклад, собрались истинные любители головоломок.
Демейн — высокий и тощий, с пушистой бородкой и собранными в хвост вьющимися темно-русыми волосами — вывел изображение «Головоломки галантерейщика» на большой экран за своей спиной. Он сообщил слушателям, что недавно принял решение взяться за эту задачу вместе со своими аспирантами. «Я не верил, что все это правда», — сказал он. Вопреки ожиданиям, однако, он и его ученики обнаружили, что можно преобразовать любой многоугольник в любой другой многоугольник той же площади, выполняя разбиения в духе «Головоломки галантерейщика». Аудитория зааплодировала — что не так часто случается в высших кругах вычислительной геометрии. Ведь слушатели Демейна стали свидетелями того, как была решена поистине культовая задача! И сделал это блестящий Демейн!
Та конференция в Атланте, называвшаяся «Gathering for Gardner», «Собрание для Гарднера», представляла собой собрание, где в максимальной степени были способны оценить доклад Демейна. Она проводится раз в два года, дабы отдать дань уважения человеку, который во второй половине XX столетия революционизировал занимательную математику. Мартин Гарднер, умерший совсем недавно, в 2010 году, в возрасте 95 лет, вел в 1957–1981 годах ежемесячную математическую колонку в журнале «Scientific American». То был период колоссального научного прогресса — космических полетов, новых информационных технологий, достижений в генетике, — и несмотря на это, внимание читателя неизменно привлекали написанные живым и ясным языком гарднеровские заметки. «По-моему, Гарднер проявлял уважение к веселой стороне математики, на которую редко обращают внимание в математических кругах, — сказал мне Демейн, когда я подошел к нему после его доклада. — Люди все время стараются быть уж очень серьезными. А вот моя цель — найти элемент забавы во всем, что я делаю».
Тогда в Атланте Демейн не стал объяснять подробности своего доказательства универсальности разбиений в стиле «Головоломки галантерейщика», но сказал, что разбиение одного многоугольника, позволяющее сложить из него другой, поворачивая куски на шарнирах, выглядит далеко не всегда симпатично — и часто оказывается малопригодным с практической точки зрения. Демейн сейчас занят приложением своей теоретической работы по шарнирным разбиениям к созданию роботов, которые смогут изменять свою форму, складываясь и раскладываясь, подобно героям книги комиксов и киносериала «Трансформеры», где роботы превращаются в различные машины.
* * *
Та конференция была восьмым по счету «Собранием для Гарднера», или G4G, и ее логотип, придуманный дизайнером Скоттом Кимом, представляет собой перевертыш, или амбиграмму.
После переворачивания вверх ногами она не меняется. Ким — специалист по прикладной математике, переквалифицировавшийся в изобретателя головоломок, — создал стиль симметричной каллиграфии в 1970-х годах. (Одновременно, и совершенно независимо, с художником Лэнгдоном.) Амбиграммы не обязательно должны оставаться неизменными при повороте именно на 180 градусов — подойдет любая симметрия или тайнопись. Математики питают особую любовь к записям такого типа, поскольку они перекликаются с их собственными поисками скрытых структур и симметрий.
На конференции G4G невозможно было отделаться от мысли, что математика отвращает наступление старческого слабоумия. Многим из приглашенных было более 70 лет, а некоторым — за 80 и даже за 90. В течение более полувека Гарднер переписывался с тысячами читателей, многие из них были знаменитыми математиками, а некоторые стали его близкими друзьями. Реймонд Смулльян, которому 88 лет, является ведущим мировым специалистом по логическим парадоксам. Он предварил свое выступление такой фразой: «Прежде чем я начну говорить, позвольте мне кое-что сказать». Стройный, одетый с изящной небрежностью, с мягкими белыми волосами и воздушной бородой, Смулльян часто развлекал гостей конференции, играя на фортепиано в отеле. Кроме того, он показывал волшебные фокусы ничего не подозревающим прохожим, а однажды вечером за ужином заслужил овации, исполнив экспромтом комедийную сценку.
Другой участник конференции — Иван Москович. Ему 82, и он поразительно похож на постаревшего Винсента Прайса
[45] — в безупречно строгом темном костюме, со сверкающими глазами, торчащими карандашом усами и шевелюрой зачесанных назад седых волос. Москович — тоже изобретатель головоломок. Он показал мне свое самое последнее творение, получившее название «Ты и Эйнштейн». Его мечта — как и каждого, кто увлечен этим занятием, — состоит в том, чтобы придумать головоломку, которая вызовет новую волну массового помешательства. До сих пор имели место всего четыре всемирных волны лихорадки по поводу головоломок с математическим уклоном: танграмы, игра в пятнашки, кубик Рубика и судоку. Сегодня первенство по прибыльности держит кубик Рубика. С момента его изобретения Эрнё Рубиком в 1974 году было продано более 300 миллионов штук! Помимо чисто коммерческого успеха, этот ярко раскрашенный разноцветный куб оказался неувядающим элементом массовой культуры. Он занимает беспрецедентное положение в мире головоломок, и нет ничего удивительного в том, что его популярность ощущалась и на конференции G4G в 2008 году. Доклад о кубике Рубика в четырех измерениях вызвал бурю аплодисментов.
* * *
Исходно кубик Рубика представлял собой конструкцию из 26 меньших кубиков, собранных в большой куб размером 3 × 3 × 3. Каждый горизонтальный и вертикальный «срез» может независимо вращаться. После того как все цвета граней перемешаны, задача состоит в том, чтобы вращением «срезов» добиться, чтобы каждая сторона куба состояла целиком из квадратиков одного цвета. Всего имеется шесть цветов, по одному для каждой стороны. По мнению Московича, Эрнё Рубик проявил гениальность дважды. Не только сама идея куба была гениальной, но и способ, которым отдельные элементы соединены друг с другом, — выдающееся инженерное решение. Если разобрать кубик Рубика, то оказывается, что внутри нет никаких специальных механических приспособлений, удерживающих отдельные детали вместе, — каждый из кубиков содержит часть центральной сцепляющей сферы.