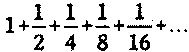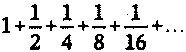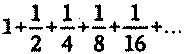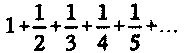Как и в приведенном парадоксе, во всех парадоксах Зенона явно абсурдные заключения получаются в результате бесконечного разбиения непрерывного процесса движения на дискретные события. Ахиллу, прежде чем он сможет догнать черепаху, надо совершить бесконечное число дискретных «шагов». Парадокс возникает из допущения, что невозможно совершить бесконечное число «шагов» за конечное время.
У древних греков, впрочем, не было глубокого математического понимания бесконечности, позволявшего заключить, что это предположение ошибочно. Можно совершить бесконечное число «шагов» за конечное время. Основное требование состоит в том, что эти «шаги» должны становиться все короче, а их прохождение — занимать все меньше времени, так что при этом как расстояние, так и время стремятся к нулю. Хотя это и необходимое условие, оно не является достаточным; «шаги» также должны уменьшаться достаточно быстро.
А теперь вернемся к Ахиллу и черепахе. Пусть, например, герой бежит со скоростью, в два раза превышающей скорость черепахи, и пусть точка В на один метр впереди точки А. Когда Ахилл достигает точки В, черепаха прошла полметра до С. Когда Ахилл достигает точки С, черепаха прошла еще четверть метра и попала в точку D и т. д. Полное расстояние в метрах, которое пробежит Ахилл, пока не догонит черепаху, равно
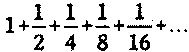
Если бы Ахиллу требовалась секунда, чтобы пройти каждый из этих «шагов», то прохождение всего расстояния заняло бы у него вечность. Но дело обстоит не так. Предположим, он бежит с постоянной скоростью, тогда ему понадобится секунда, чтобы пробежать метр, полсекунды — чтобы пробежать полметра, четверть секунды — чтобы пробежать четверть метра и т. д. Таким образом, время в секундах, которое потребуется ему для того, чтобы догнать черепаху, описывается той же самой суммой:
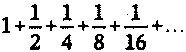
Когда и время, и расстояние описываются последовательностью, каждый член которой в два раза меньше предыдущего, их суммы одновременно сходятся к определенному конечному значению — в нашем случае к 2 секундам и 2 метрам. Итак, в конце концов выясняется, что Ахилл все же догонит черепаху.
Впрочем, не все парадоксы Зенона решаются с помощью математики бесконечных рядов. В «парадоксе дихотомии» бегун отправляется из А в В. Назовем первую точку, которую он пройдет после того, как выйдет из точки А, точкой С. Но чтобы попасть в С, он должен сначала пройти через точку, расположенную на полпути до С. Следовательно, С не может быть первой точкой, через которую он пройдет. Получается, нет никакой «первой точки», через которую проходит бегун, потому что всегда найдется точка, через которую он должен пройти до того. Если же нет первой точки, через которую проходит бегун, говорит нам Зенон, значит, бегун никогда не сможет сдвинуться с точки А.
Согласно легенде, для опровержения этого парадокса киник Диоген молча встал и прошел от А до В, тем самым продемонстрировав, что движение возможно. Но зеноновский парадокс дихотомии не удается так просто списать со счета. За два с половиной тысячелетия, в течение которых ученые чесали затылки, никто не смог полностью разрешить эту загадку. Часть проблемы состоит в том, что непрерывная линия не допускает адекватного представления последовательностью ни из бесконечного числа дискретных точек, ни из бесконечного числа малых интервалов. Подобным же образом непрерывный промежуток времени невозможно адекватно представить бесконечным числом дискретных временных интервалов. Концепции непрерывности и дискретности не хотят уживаться друг с другом.
Десятичная система предоставляет нам чудесный пример парадокса в духе Зенона. Каково самое большое число, меньшее единицы? Это не 0,9, потому что 0,99 больше него, но при этом меньше единицы. Но это и не 0,99, поскольку 0,999 еще больше, но все равно меньше единицы. Единственный возможный кандидат — это периодическая десятичная дробь 0,9999…, где многоточие означает, что девятки продолжаются неограниченно. Здесь-то и заключается парадокс. Искомое число не может быть равно 0,9999…, потому что 0,9999… совпадает с числом 1!
Вот как на это можно смотреть. Если бы 0,9999… было числом, отличным от 1, то между ними был бы некий интервал на числовой прямой. А тогда было бы возможно втиснуть в этот интервал еще какое-то число — число больше 0,9999… и меньше 1. Но что это могло бы быть за число? Подобраться к 1 ближе, чем 0,9999…, нельзя. Таким образом, если 0,9999… и 1 неразличимы, то они должны совпадать. Сколь бы странным такое ни казалось, 0,9999… = 1.
Так какое же самое большое число, меньшее единицы? Единственное удовлетворительное заключение, которое можно сделать, исходя из этого парадокса, состоит в том, что самого большого числа меньше единицы не существует.
* * *
Парадокс, связанный с гонкой Ахилла за черепахой, разрешился, когда мы записали продолжительности его «шагов» как сумму с бесконечным числом слагаемых. Такие суммы известны также как бесконечные ряды. При сложении членов бесконечного ряда возможны два случая в зависимости от того, конечным или бесконечным будет предел, то есть то число, к которому сумма подходит все ближе и ближе по мере прибавления все новых членов. Если предел конечный, то ряд называется сходящимся. Если нет — ряд называется расходящимся.
Например, мы видели, что ряд
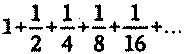
сходится, и сходится он к числу 2. Кроме того, много рядов, как мы видели, сходятся к числу π.
Напротив, ряд
расходится, устремляясь в бесконечность.
Когда я учил математику, одним из моих любимых упражнений было занятие с бесконечными рядами, состоявшее в выяснении того, сходится данный ряд или расходится. Меня всегда поражало, что при всем колоссальном различии между сходимостью и расходимостью — различии между конечным числом и бесконечностью, отличающимися на бесконечность, — детали, определяющие поведение ряда, порой кажутся совершенно несущественными.
Взглянем на гармонический ряд:
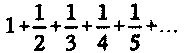
Числитель каждого из членов здесь равен 1, а знаменатели — просто все натуральные числа. С виду ряд должен бы сходиться. Каждый следующий член в этом ряду делается все меньше и меньше, так что можно было бы ожидать, что сумма всех членов окажется ограниченной некоторым фиксированным числом. Однако же гармонический ряд — расходящийся, подобно замедляющейся, но не останавливающейся улитке. Сумма первых 100 членов ряда едва превышает 5. Сумма впервые превышает число 100 только после суммирования 15 092 688 622 113 788 323 693 563 264 538 101 449 859 497 членов. Эта упорная улитка будет продолжать свое движение к свободе, преодолевая любое заданное ей расстояние. В конце концов ряд достигнет миллиона, затем миллиарда, уходя все далее и далее к бесконечности. (Доказательство этого факта приводится в приложении 5 на сайте, посвященном этой книге.)