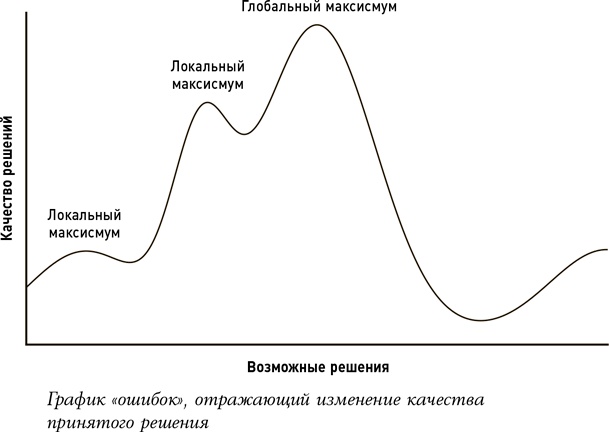
В конечном итоге вы найдете наилучшее решение из всех возможных перестановок. И не важно, какие соседние города вы меняете местами: оно останется таковым. Именно здесь заканчивается ваше восхождение на холм. Означает ли это, что вы нашли единственно возможный наилучший маршрут? К сожалению, нет. Вы могли найти только так называемый локальный максимум, но не глобальный максимум всех вероятностей. Холмистый ландшафт к тому же окутан туманом. Вы можете сделать вывод, что стоите на вершине холма, только на основе того факта, что вокруг вас видны уходящие вниз склоны. Но, возможно, за долиной есть гора и повыше, скрытая за облаками.
Представьте себе лобстера, застрявшего в ловушке: бедное животное не понимает, что для того, чтобы выбраться, ему нужно вернуться к центру клетки, то есть забраться в нее поглубже. Ловушка для лобстеров не что иное, как локальный максимум из проволоки – локальный максимум, который убивает.
В ситуации с планированием отпуска локальные максимумы, к счастью, не столь фатальны, но несут в себе тот же смысл. Даже если нам удастся найти решение, которое нельзя будет улучшить за счет мелких ухищрений, вполне вероятно, что мы по-прежнему упускаем глобальный максимум. Истинно наилучший маршрут может потребовать полного изменения плана всей поездки: придется, к примеру, поменять местами целые континенты или направляться с востока на запад, а не с запада на восток. Нам порой приходится временно ухудшить наш вариант, если мы хотим продолжать искать лучший. И случайность обеспечивает стратегию для этого – несколько стратегий, если быть точным.
Преодолеть локальный максимум
Один из таких способов – улучшить ваше восхождение на холм с помощью того, что называется «дрожание»: если вы чувствуете, что застряли на месте, попробуйте немного перемешать все планы. Внесите несколько случайных незначительных изменений (даже если они будут к худшему), а затем снова вернитесь к восхождению на холм. Возможно, вы очутитесь на более высокой вершине.
Другой вариант – полностью перетасовать все планы, как только мы достигнем локального максимума, и начать восхождение на холм заново с этой новой случайно выбранной отправной точки. Этот алгоритм имеет подходящее название «случайный перезапуск восхождения», или – еще более красочно – «восхождение наугад». Такая стратегия оказывается весьма эффективной, когда в задаче несколько локальных максимумов. Например, компьютерщики пользуются ею при дешифровке кодов, поскольку всегда есть много способов начать дешифровку, которые выглядят многообещающе, а в итоге заводят в тупик. Если в ходе дешифровки у вас получается текст, отдаленно напоминающий нормальный русский язык, это еще не значит, что вы на правильном пути. Так что порой лучше не привязываться к изначально выбранному направлению, каким бы правильным оно вам ни казалось, и начать все с нуля.
Но есть еще и третий способ: вместо того чтобы полностью положиться на волю случая, когда ты зашел в тупик, прибегайте к помощи случайности в каких-то мелочах каждый раз, когда принимаете решение. Эта техника, придуманная все той же командой из Лос-Аламоса, которая разработала метод Монте-Карло, получила название «алгоритм Метрополиса». Алгоритм Метрополиса, так же как и «восхождение на холм», работает за счет мелких перестановок в решении, но с одним большим отличием: в любой заданной точке он может принять плохие перестановки наравне с хорошими.
Давайте попробуем применить этот метод к планированию нашего отпуска. Мы снова попробуем скорректировать маршрут, меняя местами разные города. Если получившаяся случайным образом перестановка приводит к улучшению маршрута, мы принимаем ее и продолжаем процесс дальше с этой точки. Но, если изменение приводит к небольшому ухудшению, все равно остается шанс, что мы примем его (хотя чем хуже изменение, тем меньше этот шанс). Таким образом, мы не застреваем в одном локальном максимуме надолго: в конце концов, мы испробуем другое решение, пусть это и окажется немного дороже, и продолжим нашу работу по созданию нового и лучшего плана.
Не важно, будет ли это «дрожание», случайный перезапуск или готовность к временному ухудшению, случайность остается невероятно полезным способом избегать локальных максимумов. Шанс – это не только конкурентоспособный метод решения жестких проблем оптимизации; во многих случаях он играет решающую роль. Но некоторые вопросы еще остаются открытыми. Какой процент случайности нужно использовать? И когда? И – учитывая, что такие стратегии, как алгоритм Метрополиса, могут менять наш маршрут до бесконечности, – как вообще понять, что можно заканчивать? Окончательный ответ на эти вопросы немедленно даст исследователям, работающим над вопросом оптимизации, новую пищу для размышлений.
Имитация отжига
В конце 1970-х – начале 1980-х годов Скотт Киркпатрик считался физиком, а не специалистом в области информатики. В частности, его интересовала статистическая физика, в которой случайностью объяснялись некоторые явления природы, например физика отжига – то, как материалы меняют свое состояние в процессе нагрева или охлаждения. Пожалуй, самой интересной характеристикой отжига является скорость охлаждения вещества, которая оказывает огромное влияние на его конечную структуру. Как писал Киркпатрик:
Выращивание монокристалла из расплава происходит путем аккуратного отжига, когда вещество сперва расплавляют, а затем медленно понижают температуру, долгое время удерживая ее в области точки замерзания. Если этого не сделать и позволить веществу выйти из равновесного состояния, то у полученного кристалла будет множество дефектов или вещество вовсе превратится в стекло без какой-либо кристаллической структуры.
Киркпатрик в то время работал в компании IBM, где самой сложной и важной проблемой было нанесение электросхем на чипы, производимые компанией. Проблема была громоздкой и труднорешаемой: существовало множество путей решения, и при этом имелись некоторые сложные ограничения. Так, например, в общем и целом стоило располагать элементы близко друг к другу, но не слишком, чтобы оставалось место для соединения. И каждый раз, как что-то сдвигалось, приходилось по новой рассчитывать, как все соединения будут работать при гипотетическом новом расположении.
В те времена процессом руководил своего рода тайный гуру компании IBM. Киркпатрик вспоминает: «Тот парень мог напихать на чип больше всего микросхем… и у него был весьма загадочный способ объяснять, что он делает. Он реально не любил об этом рассказывать».
Друг и коллега Киркпатрика Дэн Гелатт проявил живой интерес к этой проблеме и увлек ею и самого Скотта, с которым случилось внезапное прозрение. «Способ изучения [физических систем] заключался в том, чтобы нагреть их, затем охладить и дать системе возможность самоорганизоваться. С данной точки зрения, это выглядело совершенно естественным способом решения всех типов проблем оптимизации, как если бы количество степеней свободы, которые вы пытаетесь организовать, были бы маленькими атомами, спинами или чем там еще».

