Один из самых запоминающихся блефов в игре высокого уровня произошел тогда, когда Том Дван на турнире по техасскому холдему разыгрывал $479 500, имея самую худшую из возможных комбинаций – 2: 7, в то время как его оппонент Сэмми Джордж, образно выражаясь, буквально держал выигрыш в руках.
Рекурсии в покере – опасная игра. Вы, конечно, не хотите отстать ни на шаг от вашего оппонента, но – что также крайне важно – не стоит и слишком сильно опережать его. «Существует правило, гласящее, что вы должны играть только на один уровень выше вашего оппонента, – объясняет профессиональный игрок в покер Ванесса Руссо. – Если вы слишком опережаете ваших оппонентов, то вы начинаете думать, что они имеют информацию, которой на самом деле у них нет, и в этом случае они уже никак не смогут получить ту информацию, которую – как вам хотелось бы – они могли бы извлечь из ваших действий». Иногда профессионалы покера могут намеренно втравливать своего противника в развернутую рекурсию, в то время как сами играют по академическим правилам без всякой психологической подоплеки. В этом случае говорят о заманивании оппонентов в войну выравнивания против самих себя.
(Вовлечение противника в бесплодные рекурсии может оказаться эффективной стратегией также и в других играх. Один из самых ярких, странных и захватывающих эпизодов в истории шахматного противостояния человека и машины произошел в 2008 году во время сражения американского гроссмейстера Хикару Накамура с ведущей шахматной компьютерной программой Rybka. В игре, где каждая из сторон получала всего три минуты на все ходы или ей автоматически присуждался проигрыш, преимущество, разумеется, отдавалось компьютеру, способному оценить миллионы комбинаций в секунду и сделать ход без использования мышц. Но Накамура мгновенно создал на доске затор, делая повторяющиеся, бессмысленные ходы настолько быстро, насколько позволяло нажатие кнопки на часах. В то время как компьютер впустую тратил драгоценные мгновения на бесплодные поиски победного варианта, которого даже и не существовало, и упорно пытался предвидеть все возможные будущие ходы противника, Накамура играл в шахматы фактически спустя рукава. Когда компьютер уже почти исчерпал свое время и начал переставлять фигуры так, чтобы хотя бы не проиграть по часам, Накамура наконец открыл свою позицию и разгромил соперника.)
Как же профессиональные игроки выходят из ситуации, зная опасность рекурсии? Они используют теорию игр. «Порой вы можете придумать причины, объясняющие, почему вы играете именно так, но зачастую ваши худшие игры становятся таковыми по причинам, которые на самом деле не стоит и упоминать, – объясняет Дэн Смит. – Я прикладываю немало усилий, чтобы воспользоваться базовым уровнем теории в большинстве ситуаций… Я всегда начинаю со знания или попытки узнать, что такое Нэш».
Так что же такое Нэш?
Достижение равновесия
Вы знаете правила, и я их тоже знаю…
Мы знаем игру, и мы собираемся в нее сыграть.
Рик Эстли
Теория игр охватывает невероятно широкий спектр сценариев сотрудничества и конкуренции, но начиналось все с покера – соревнования между двумя людьми, где выигрыш одного из игроков означает проигрыш другого. Математики, анализирующие эти игры, пытаются найти так называемое равновесие – некий набор стратегий, которым оба игрока могут следовать таким образом, чтобы ни один из игроков не хотел бы изменить собственную игру, даже учитывая игру соперников. Это называется равновесием потому, что это состояние стабильности: никакое количество дальнейших обдумываний не предоставит никому из игроков другого выбора. Я удовлетворен своей стратегией, принимая во внимание вашу, а вы довольны вашей стратегией, учитывая мою.
Например, в детской игре «Камень, ножницы, бумага» равновесие достигается примерно каждую треть времени при совершенно случайном выборе одного из названных жестов. Устойчивым это равновесие делает то, что раз оба игрока приняли эту
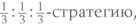то нет ничего лучше, чем и в дальнейшем ей следовать. (Если даже мы попытаемся чаще выбирать, скажем, камень, то наш противник быстро это заметит и начнет чаще выбирать бумагу, что заставит нас чаще выбирать ножницы; и так далее – до тех пор, пока вновь не восстановится равновесие
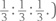
В одном из основополагающих выводов теории игр математик Джон Нэш доказал в 1951 году, что каждая игра двух игроков имеет по крайней мере одно равновесие. Это крупное открытие принесло Нэшу в 1994 году Нобелевскую премию по экономике (и послужило поводом для написания книги и создания фильма «Игры разума» о жизни Нэша). Такое равновесие теперь часто называют равновесием Нэша, и именно этот «Нэш» всегда пытается отследить Дэн Смит.
На первый взгляд, тот факт, что равновесие Нэша всегда существует в поединках между двумя игроками, казалось бы, должно принести нам некоторое облегчение от рекурсий зеркальной комнаты, которые характерны для покера и многих других привычных соревнований. Когда мы чувствуем, что падаем в рекурсивную кроличью нору, у нас всегда есть возможность покинуть голову оппонента и поискать равновесие, напрямую ведущее к лучшей стратегии, предполагающей рациональную игру. В игре «Камень, ножницы, бумага» попытка прочесть по лицу оппонента, что он выберет в следующий раз, может оказаться не слишком полезной, если вы знаете, что даже простой случайный выбор означает непобедимую стратегию в долгосрочной перспективе.
В более общем смысле равновесие Нэша выражает прогноз стабильного долгосрочного результата для любого набора правил. Таким образом, этот подход – бесценный инструмент не только для прогнозирования и формирования экономической политики, но также и для социальной политики в целом. Как утверждает лауреат Нобелевской премии экономист Роджер Майерсон, равновесие по Нэшу «имело такое фундаментальное и всеобъемлющее влияние на экономику и социальные науки, которое сопоставимо с открытием двойной спирали ДНК в биологии».
Однако информатика усложняет эту ситуацию. В самом широком смысле объектом исследований в математике является истина; объектом исследований в информатике является сложность. Нетрудно заметить, что недостаточно иметь решение проблемы, если такая проблема трудноразрешима.
В контексте теории игр знание, что равновесие существует, не говорит нам, что это такое или как его найти. Как пишет ученый Калифорнийского университета в Беркли Христо Пападимитриу, теория игр «предсказывает равновесное поведение агентов, как правило, без учета того, каким образом такое состояние будет достигнуто, оставляя это в первую очередь на усмотрение того, кто будет этим заниматься». Стэнфордский ученый Тим Ругарден вторит ему, выражая свою неудовлетворенность доказательством Нэша о том, что равновесие всегда существует. «Хорошо, – говорит он, – мы ведь программисты, не так ли? Тогда дайте нам что-нибудь, что мы можем использовать. Не надо говорить мне, что это где-то там; скажите мне, как это найти». Итак, исходное поле боя в теории игр породило теорию алгоритмических игр, то есть изучение теоретически идеальных игровых стратегий переросло в изучение того, как машины (и люди) подошли к формированию стратегий игр.
