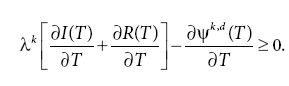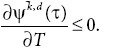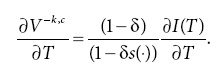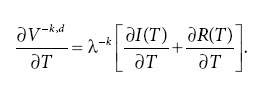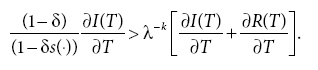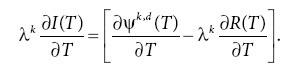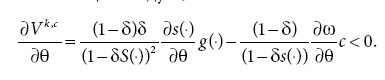b) Предположим, что равновесие со взаимным сдерживанием (λk, Т) существует для каждого Т и потенциальных инвестиций в военную силу ψk,d (T), является строго положительным для k = i, j (без потери общности). Тогда, если оптимальное для клана количество привилегий не равно нулю, его чистый средний выигрыш максимизируется при равновесии со взаимным сдерживанием (λk, Т *) таком, что T * < τ и λk ∂I(T *)/∂(T) = ∂ψ—k,d (T *)/∂T —λk ∂R(T *)/ ∂T.
Доказательство. При равновесии со взаимным сдерживанием (λk, Т) оптимальные для клана k инвестиции таковы, что ограничение по стимулу в условии VIII.1 ICC-k является обязательным на самой большой осуществимой инвестиции для клана – k, т. е. λ—k[I(T) + R(T)]. Это локальное обязательное ограничение имплицитно определяет ψ—k как функцию от Т, т. е. ψ—k,d (T). Наиболее выгодное для клана k равновесие со взаимным сдерживанием (Т) – это равновесие, которое максимизирует его доход за период при равновесии со взаимным сдерживанием, т. е. H(T) = λk[I(T) + R(T)] – ψ —k,d (T). Условием первого порядка для максимизации является:
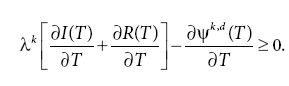
Оцениваемое при Т = τ, это условие первого порядка выполняется тогда и только тогда, когда
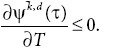
Равновесное вложение в военную силу ψk,*(τ) возрастает в Т, если ∂V-k,c/∂T > ∂V-k,d /∂T. По теореме об огибающей
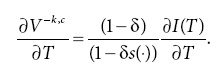
Сходным образом
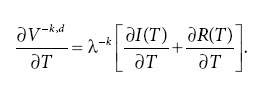
Отсюда ∂V—k,c/∂T > ∂V—k,d/∂T тогда и только тогда, когда
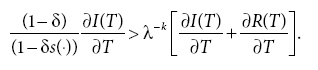
Оцениваемая при Т = т правая сторона этого неравенства равна нулю, а левая сторона строго положительна. Таким образом, равновесная инвестиция в военную силу возрастает в Т = τ, т. е. ∂ψk,d(τ/∂T > 0, подразумевая, что ожидаемая кланами полезность не максимизируется при эффективном количестве привилегий.
Что касается второго утверждения, ожидаемая кланом к полезность максимизируется при равновесии со взаимным сдерживанием, в котором
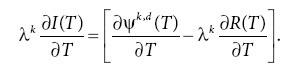
Что и требовалось доказать.
Из этой теоремы следует, что неэффективное равновесие со взаимным сдерживанием с большей вероятностью будет существовать, если внешняя угроза слабее. В частности, ожидаемая ценность положения контролирующего клана возрастает с ослаблением внешней угрозы. Это предполагает более широкий диапазон параметров, на котором эффективное равновесие со взаимным сдерживанием характеризуется положительными инвестициями в военную силу, что равноценно наличию положительного числа сторонников (напомним, что инвестиции в военную силу приравнены к вербовке сторонников.)
Формально в пределе, когда θ → 0 (и следовательно s(∙) → 1 и ω(∙) → 1 для ψk = 0), c(1 —δ) →0 и R(T) → 0 равновесное число сторонников должно быть положительным если для k = i или j, ∃ ψk ≤λk [I(T) + R(T)] таково что sk,w (ψk, 0) > λk, т. е. существует реальное число сторонников, которые делают вероятность победы клана k, sk,w (∙) выше, чем его доля прибылей λk, когда у другого клана нет сторонников.
Теорема VIII.2
Предположим, что для ∀T ∈ [0, τ] существует равновесие со взаимным сдерживанием (λk, T) с положительным равновесным инвестированием в военную силу. Для обоих кланов количество оптимальных привилегий Т*(θ) является неубывающим в θ.
Доказательство. Любое сокращение в Vk,c () ослабляет ограничения взаимного сдерживания и делает большее количество привилегий оптимальным для обоих кланов. Поскольку θ влияет только на Vk,c (), для доказательства теоремы достаточно показать, что ожидаемая полезность для контролирующего клана убывает в θ. Ожидаемая полезность для контролирующего клана представляет собой функцию ценности для задачи OP, определенной выше. Чтобы увидеть, что она убывает в θ, определим g(∙) = I(T) – ψ – cω(∙)(> 0) и вспомним, что ∂s(∙/∂θ< 0 и ∂ω∙/∂θ> 0. Из этих соотношений и теореме об огибающей следует, что
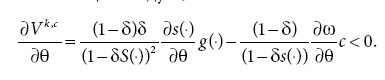
Что и требовалось доказать.
ПРИЛОЖЕНИЕ VIII.2 СУЩЕСТВОВАНИЕ РАВНОВЕСИЯ СО ВЗАИМНЫМ СДЕРЖИВАНИЕМ
Каковы условия, при которых равновесие со взаимным сдерживанием не существует? Из условия VIII.1 следует, что такое равновесие (λk, Т) не существует, если один клан считает выгодным вступать в конфронтацию, когда другой клан инвестирует все свои ресурсы в укрепление своей военной силы. Иначе говоря, если для k = i или j, ∃ ψk ≤ λ k [I(T) + R(T)] такое, что ψ-k=λ-k [I(T)+R(T)], δV k,d(λ k, T, ψk,d)<δV k,w(ψ k,ψ-k)V k,c(T, θ) – (c + ψ k -ψk,d))(1-δ).