В пределе, когда R(T) →0, θ→ 0 (из чего следует, что s()→ 1 и ω()→ 0 и д → 1), равновесие со взаимным сдерживанием (λk, Т) не существует тогда и только тогда, когда для k = i или j, λk < sk,w (•) для некоторого осуществимого ψk и всех осуществимых ψ-k. Таким образом, равновесие со взаимным сдерживанием (λk, Т) для размещения λk не существует, если один клан имеет достаточно сторонников, так что вероятность того, что он победит при конфронтации, выше, чем его доля в доходе.
ПРИЛОЖЕНИЕ VIII.3
СГОВОР И ИГРЫ ПОДЕСТАТА
Игра со сговором
В какой степени клан может ex ante придерживаться обещания вознаградить ex post подеста, который оказывает ему военную помощь? Обозначим как νi (mi, mk; mi) вероятность того, что игрок i (клан или подеста) выиграет войну против j или K, учитывая сравнительную военную силу mj, mk и mi. Вероятность победы i убывает в mj и mк и возрастает в mj. (для простоты изложения я опущу параметр mj в последующих уравнениях). Если игрок участвует в военной конфронтации, ему приходится нести расходы с. Vj – чистая дисконтированная стоимость контроля над Генуей для игрока i. Предположим, что местные кланы выигрывают больше, чем подеста, от контроля над городом, т. е. Vj > Vp, если игрок i – клан
[259].
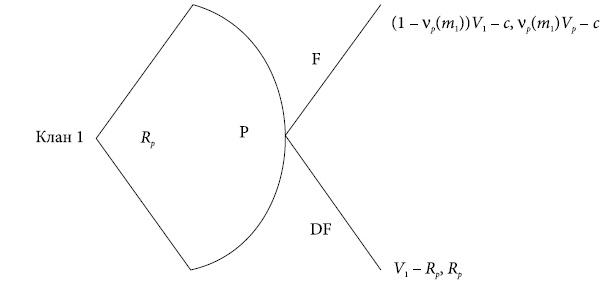
РИС. VIII.2. Игра в сговор
Посмотрим, что произойдет после того, как клан (скажем, клан 1) и подеста вступят в сговор против другого клана и получат контроль над городом (рис. VIII.2). Контролирующему клану придется решать, какое вознаграждение Rp > 0 дать подеста. Как только эта награда объявлена, подеста может либо принять, либо отвергнуть ее и бороться с кланом за контроль над городом. Если он ее принимает, выигрыши составляют V1 – Rp для клана и Rp для подеста. Если он отвергает ее и борется, ожидаемый выигрыш для каждого – вероятность победы минус издержки на получение контроля минус издержки на войну, а именно (1 – vp(m1))V1 – c и vp(m1)Vp – c.
Клан не сочтет выгодным предложить Rp выше, чем то, что требуется, чтобы сделать безразличным выбор между борьбой и отказом от борьбы, т. е. V1 – Rp > (1 – v(m1))V1 – c. Следовательно, он предложит Rp ≤ vp(m1)V1 + c. Если подеста получает платеж, равный чистой ожидаемой стоимости борьбы против клана, а именно Rp ≥ vp(m1)Vp – c, он сочтет оптимальным для себя не вступать в борьбу. Таким образом, при любом совершенном по подыграм равновесии клан не предложит больше суммы, необходимой для того, чтобы выбор между вступлением в борьбу и отказом от нее был для подеста безразличен, а именно Rp = vp(m1)Vp – c. Отсюда следует, что единственное совершенное в подыгре равновесие – то, в котором клан предлагает Rp = vp(m1)V1 – c, а стратегия подеста заключается в том, чтобы вступить в борьбу, если ему заплатят меньше этой суммы, и не вступать в борьбу, если ему заплатят хотя бы эту сумму. Выигрыши, связанные с этим равновесием, составляют V1 – Vpс для клана и Vpс для подеста, где Vpс=Max {0,vp (m1)Vp – с}.
Из этого анализа следует, что когда происходит сговор, вознаграждение подеста зависит от его военного потенциала
[260]. В частности, при любом равновесии подеста не получит больше чистой дисконтированной стоимости военной конфронтации с кланом. Таким образом, ex ante – прежде чем произойдет сговор – клан не может убедительно пообещать выплатить подеста ex post вознаграждение, большее, чем эта сумма. Когда vp(m1)Vp – c ≤ 0, например, клан не может дать никаких достоверных обещаний вознаградить подеста. Чем слабее подеста, тем слабее способность клана сделать его ex ante обещание награды достоверным
[261].
Игра с подестатом
Ограничение военного потенциала подеста (по сравнению с военным потенциалом клана) предполагает, что его военная сила сама по себе становится менее действенной в удержании одного клана от вступления в конфронтацию с другим кланом. Чтобы увидеть, как все-таки можно удерживать клан от конфронтации, рассмотрим две проблемы: мотивацию подеста помогать клану, который проигрывает при межкланвой конфронтации, и мотивацию клана бороться вместе с подеста.
Пусть Ii – доход клана i за период, если никакой межклановой военной конфронтации не происходит, W – жалованье подеста и δ – фактор временного дисконтирования
[262]. Игра с подестатом раскрывает, как межклановая игра может быть изменена путем введения подеста вопреки потребности ограничивать его военную силу (рис. VIII.3).
Эта повторяющаяся игра начинается, без потери общности, с того, что клан 1 должен решить, вступать ли в конфронтацию с кланом 2. Если клан 1 решает вступить в конфронтацию, клан 2 должен выбрать, сражаться ему или нет. В любом случае подеста может ответить тем, что помешает клану 1 захватить контроль над городом (действие, обозначенное какр), тем, что не станет мешать клану 1 (dp) или вступит в сговор с ним (со). Если подеста вступает в сговор с кланом 1, я для простоты изложения предполагаю, что клан 2 не может захватить контроль над городом и что подеста и клан 1 играют в игру в сговор (рис. VIII.2). Поскольку в игре в сговор есть единственное совершенное в подыгре равновесие, рис. VIII.3 представляет только выигрыши, связанные с этим равновесием.



