Сагредо. Итак, если я хорошо понял, я могу тотчас же вычислить длину веревки, укрепленной на любой огромной высоте, хотя бы точка подвеса ее и не была видима, раз только я могу наблюдать движение ее нижнего конца. Для этого мне понадобится лишь привязать к нижнему концу достаточный груз, который будет качаться взад и вперед, и в то время, как кто-либо из моих друзей будет считать эти качания, самому наблюдать и считать одновременно качания другого маятника, длина которого равняется точно одному локтю. Из чисел качания этих двух маятников за один и тот же промежуток времени я и вычислю искомую длину нити. Положим, что в то время, как мой друг насчитал двадцать качаний длинного маятника, я нашел, что мой маятник, длиною в один локоть, совершил их двести сорок; возведя числа двадцать и двести сорок в квадрат, получим 400 и 57 600, из чего заключим, что длинный маятник содержит 57 600 таких частей, которых в меньшем, длиною в один локоть, содержится 400; а разделив 57 600 на 400, получим число 144; таким образом я узнаю, что веревка имеет длину в 144 локтя.

Маятник в движении
Сальвиати. Вы не ошибетесь и на толщину одного пальца, особенно если сосчитаете большое число качаний.
Сагредо. Как часто даете вы мне случай, синьор, удивляться богатству и вместе с тем щедрости природы, делая совершенно новые интересные выводы из простых, известных и, скажу, даже тривиальных вещей, выводы, далекие от того, что может представить воображение. Тысячи раз наблюдал я качание, в особенности церковных паникадил, подвешенных часто на очень длинных цепях и почему-либо совершающих незначительные движения. Однако самое большее, что я вывел из этих наблюдений, это то, что мнение, будто такие движения поддерживаются окружающей средою – в данном случае воздухом, – неосновательно. Мне казалось невозможным, чтобы воздух имел такое правильное движение или чтобы ему нечего было делать, кроме как проводить час за часом в раскачивании с такою размеренностью свешивающихся тяжестей. Но то обстоятельство, что одно и то же тело, свешивающееся с высоты ста локтей, употребляет на прохождение больших и малых дуг при отклонении на девяносто градусов и на один градус одинаковый промежуток времени, ускользало от моего внимания и до сих пор кажется мне невозможным. Теперь я нахожусь в ожидании услышать, каким образом эти простейшие соотношения могут объяснить музыкальные проблемы, и хотя отчасти удовлетворить мою любознательность.
Сальвиати. Прежде всего необходимо установить, что каждый маятник имеет время качания столь строго определенное и ограниченное, что невозможно заставить его двигаться в период иной, нежели свойственный ему от природы. Если возьмем в руки веревку с привязанным к ней грузом и попробуем увеличить или уменьшить число качаний, то найдем, что это напрасный труд. С другой стороны, маятник, находящийся в покое, хотя бы и очень тяжелый, мы можем привести в движение и притом очень заметное простым дуновением, если мы будем приостанавливать дыхание при возвращении маятника и вновь дуть в соответствующий его качанию момент. Если при первом дуновении мы откачнем маятник от отвеса на полдюйма, то вторым дуновением по возвращении маятника назад мы сообщим ему новый толчок и так постепенно увеличим размахи; но дуть необходимо вовремя, а не тогда, когда маятник идет навстречу (в таком случае мы мешали бы, а не помогали бы движению). Многими последовательными толчками мы постепенно сообщим маятнику такой импульс, что нужна будет сила, во много раз большая, нежели дуновение, чтобы его остановить.
Сагредо. Я еще ребенком наблюдал, как один человек подобными многократными вовремя данными толчками заставлял звонить огромный церковный колокол; желая остановить его, четверо и шестеро человек хватались за веревку, но их много раз поднимало кверху, и их совместные усилия были недостаточными, чтобы сразу лишить колокол импульса, сообщенного ему регулярными толчками одного человека.
Сальвиати. Вот пример, который вместе с моей предпосылкой может быть очень подходящим для пояснения удивительных явлений в струнах цитры или струнного кимвала, которые, приходя в движение, заставляют звучать также и другие струны и притом настроенные не только в унисон, но и в октаву и квинту. Струна после удара по ней издает звук, продолжающийся все время, пока длятся ее колебания; эти колебания заставляют дрожать и колебаться прилегающий к ней воздух, сотрясения и колебания которого распространяются на большое пространство и отзываются на всех струнах того же инструмента и других соседних. Каждая струна, настроенная в унисон с первой, будучи склонна совершать колебания в одинаковые с нею промежутки времени, при первом же толчке начинает слегка колебаться; к первому толчку присоединяется второй, третий, двадцатый и т. д., все в соответственные моменты, так что, в конце концов, получается дрожание, подобное дрожанию первой струны; при этом можно ясно видеть расширение ее колебаний до размеров колебания струны, возбуждающей ее движение. Колебания, распространяющиеся по воздуху, затрагивают и приводят в движение не только струны, но и вообще все иные тела, способные колебаться и вибрировать в промежутки времени, одинаковые со звучащей струной. Если мы прикрепим к краю инструмента различные щетинки или другие тела из весьма гибкого вещества, то, ударяя по струнам инструмента, заметим, что некоторые из них будут приходить в движение, когда мы ударяем по струне, совершающей колебания в одинаковое с ними время, другие будут оставаться при этом в покое, первые же не будут колебаться при звуке иных струн.
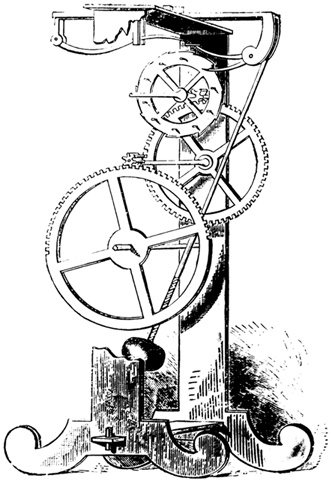
Гравюра, изображающая маятниковые часы Галилея. Результаты изучения маятников Галилей применил в практических целях для создания полезного устройства.
Если мы будем сильно водить смычком по толстой струне скрипки, приблизив к ней кубок из тонкого гладкого стекла, то, когда звучание струны будет в унисон со звучанием кубка, последний задрожит и явственно зазвучит. Распространение колебаний в среде, окружающей звучащее тело, можно ясно наблюдать, заставив звучать кубок, частью налитый водою, водя концом пальца по его краю: содержащаяся в кубке вода покроется правильными волнами. Это явление наблюдается еще отчетливее, если поставить ножку кубка на дно какого-нибудь достаточно широкого сосуда, наполнив последний водою почти до краев кубка; заставляя трением пальца звучать кубок, мы увидим, как правильные волны побегут с большой быстротой по воде и соберутся на значительном расстоянии от кубка; заставляя звучать указанным способом достаточно большой кубок, почти полный воды, я часто видел, как сперва образовывались с совершенной правильностью волны, а когда иной раз звук стекла внезапно повышался на октаву, в тот же момент каждая из волн распадалась на две – явление, ясно указывающее, что форма октавы является двойной.
Сагредо. Подобное же приходилось не раз наблюдать и мне при занятиях музыкой как для удовольствия, так и для пользы. Я долгое время находился в недоумении по поводу формы созвучий, так как мне казались недостаточными те положения и объяснения, которые обычно даются авторами сочинений о музыке. Они говорят, что диапазон, или октава, стоит в отношении двойном, а диапента, или, как мы говорим, квинта, – в отношении полуторном к основному тону и т. д.; действительно, если натянутая на монохорде струна дает основной тон, то, заставляя звучать половину струны, разделив ее пополам посредством поставленной в середине дощечки, мы получим октаву; если же мы поставим дощечку на одну треть до конца струны и, придержав меньшую часть, заставим звучать часть из двух третей струны, то получим квинту. Поэтому говорят, что в октаве созвучие состоит в отношении двух к одному, а в квинте – в отношении трех к двум. Скажу, что это рассуждение казалось мне недостаточным для того, чтобы утверждать, будто двойное и полуторное отношения являются естественными формами для диапазона и диапенты, и вот по каким основаниям. Мы можем повысить тон струны тремя способами: укорачиванием, вытягиванием или, скажем, большим натяжением и, наконец, утончением. Сохраняя одну и ту же толщину и степень натяжения, мы должны, если хотим получить октаву, разделить ее подпоркою пополам и сперва заставить звучать всю струну, а затем половину ее. Но если, сохраняя ту же толщину и длину, мы захотим получить октаву посредством большего натяжения струны, то недостаточно будет тянуть ее силою вдвое большей; для этого понадобится сила в четыре раза большая, так что если струна была первоначально натянута грузом, например в один фунт, то, чтобы получить октаву, необходимо будет подвесить груз в четыре фунта.




