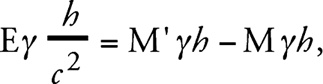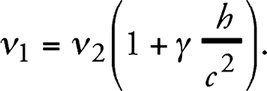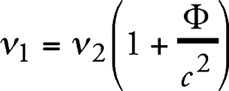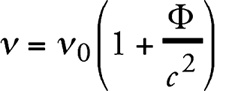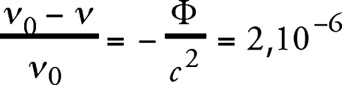1. Энергия Е, измеренная в S2, посылается в форме излучения из S2 в S1, где, согласно только что полученному результату, поглощается энергия Е × (1 + γh/с2), измеренная в S1.
2. Тело W с массой М падает из S2 в S1, и при этом совершается работа Mγh.
3. Энергия Е из системы S1 переносится на тело W, когда оно находится в S1. Благодаря этому изменяется тяжелая масса М, и пусть ее новое значение равно М’.
4. Тело W снова поднимается в S2, и при этом затрачивается работа М’ γh.
5. Энергия Е переносится с тела W на систему S2.
В результате такого кругового процесса система S1 приобрела энергию Е (γh/c2) и системой передана энергия М’γh – Mγh в форме механической работы. Следовательно, по закону сохранения энергии должно выполняться следующее соотношение:
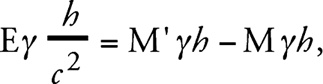
или
Окончательно получаем, что приращение тяжелой массы есть Е/c2. Другими словами, оно равно тому приращению инертной массы, которое следует из теории относительности.
Еще более естественным образом этот результат вытекает из эквивалентности системы отсчета К и К’. Согласно этой эквивалентности, тяжелая масса, определенная относительно К, в точности равна инертной массе, определенной относительно К’. Таким образом, энергия должна обладать тяжелой массой, равной ее инертной массе. Так, если с помощью пружинных весов в системе отсчета К’ взвесить массу М0, то эти весы (из-за инертности М0) покажут кажущийся вес М0γ. Если сообщить энергию Е массе М0, то, согласно предположению об инерции энергии, пружинные весы покажут (М0 + Е/c2) γ.
Согласно нашему основному предположению, то же самое должно наступить и при проведении опыта в системе отсчета К, т. е. в поле тяготения.
§ 3. Время и скорость света в поле тяжести
Пусть излучение, испускаемое в равномерно ускоренной системе отсчета К’ из S2 по направлению к S1, имеет относительно находящихся в S2 часов частоту v2. Тогда по прибытии в S1 это излучение имеет относительно находящихся там точно таких же часов частоту уже не v2, а большую частоту v1, которая в первом приближении равна
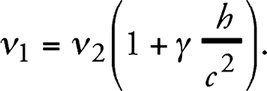
(2)
Действительно, снова вводя неускоренную систему отсчета К0, относительно которой система отсчета К’ в момент испускания света имела нулевую скорость, то S1 будет иметь относительно К0 в момент прибытия излучения в S1 скорость γ(h/с), откуда в силу принципа Допплера непосредственно получается соотношение (2).
Учитывая сделанное нами предположение об эквивалентности систем отсчета К и К’, полученное выражение справедливо и для покоящейся координатной системы К, в которой существует однородное поле тяжести, в том случае, когда в этой системе происходит описанный выше перенос энергии излучения.
Окончательно получаем, что луч света, испускаемый в области с определенным потенциалом тяготения из S2 и имеющий при его испускании частоту v2, измеренную часами, находящимися в S2, обладает при его прибытии в S1 другой частотой v1, если последняя измеряется с помощью точно таких же часов, находящихся в S1. Заменим γh через потенциал тяготения Ф, взятый в S2 по отношению к S1, потенциал которой принят равным нулю. Далее, что соотношение, полученное нами для однородного гравитационного поля, справедливо также и для полей другого вида.
В таком случае
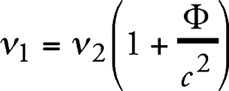
(2a)
Полученный результат (справедливый, напомним, согласно своему выводу, в первом приближении) прежде всего можно применить следующим образом. Пусть v0 – частота некоторого элементарного источника света, которая измеряется с помощью часов U, находящихся в том же месте, где и сам источник. Эта частота не зависит от расположения источника света вместе с часами. Теперь представим, что источник и часы размещены, к примеру, на поверхности Солнца (там находится наша система S2). Часть испущенного света доходит до Земли (S1), где мы часами U точно такой же конструкции, что и упомянутые выше, измеряем частоту v приходящего света. Следовательно, согласно соотношению (2а), имеем
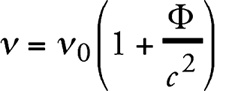
Здесь Ф – (отрицательная) разность гравитационных потенциалов между поверхностью Солнца и поверхностью Земли.
Согласно нашим представлениям, спектральные линии солнечного света должны немного сместиться по сравнению с соответствующими спектральными линиями земных источников света в красную область спектра, а именно, на относительную величину
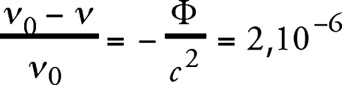
Это смещение можно было бы измерить, если бы были точно известны условия, при которых испускается солнечный свет. Но из-за того, что причины другого рода (такие как давление и температура) также влияют на положение центра тяжести спектральных линий, трудно установить, действительно ли существует выведенное выше соотношение, в котором учитывается влияние гравитационного потенциала
[14].