Мы уже близки к тому, чтобы раскрыть суть двух оставшихся составляющих на пути к пониманию, почему E = mc². Первая составляющая вряд ли вас удивит: нас будут интересовать только векторы, существующие в четырех измерениях пространства-времени. Эту концепцию легко сформулировать, но она весьма своеобразна: подобно тому как вектор может указывать на север, мы теперь имеем понятие вектора, указывающего в направлении времени. Как всегда при обсуждении пространства-времени, нам трудно мысленно представить себе эту концепцию, но это наша проблема, а не окружающего мира. Аналогия с пространственно-временной равниной, использованная нами в предыдущей главе, поможет вам сформировать мысленную картину, по крайней мере упрощенную картину пространства-времени с одним пространственным измерением. Четырехмерные векторы характеризуются четырьмя числами. Базовый вектор – тот, который соединяет две точки в пространстве-времени. Два примера такого вектора показаны на рис. 9. То, что один из векторов на рисунке указывает в направлении времени и что оба вектора исходят из одной точки, сделано исключительно ради нашего удобства. В самом общем виде вы должны представлять себе любые две точки в пространстве-времени вместе с соединяющей их стрелкой. Такие векторы – не полная абстракция. Если вы ложитесь спать в десять часов вечера и просыпаетесь в восемь часов утра, эти два события в пространстве-времени соединяет вектор, длина которого равна десяти часам, умноженным на с, указывающий в направлении времени. Более того, мы уже говорили об этих векторах в нашей книге, но не использовали такую терминологию. Например, мы столкнулись с одним очень важным вектором, когда говорили об отважном мотоциклисте, путешествующем по холмистой равнине пространства-времени с зафиксированным дроссельным клапаном. Мы пришли к выводу, что этот мотоциклист всегда перемещается в пространстве-времени со скоростью с, а также что он может выбирать только направление движения мотоцикла (хотя даже здесь у него нет полной свободы действий, поскольку ему нельзя отклоняться от северного направления более чем на 45 градусов). Мы можем представить движение мотоциклиста с помощью вектора фиксированной длины с, который указывает, в каком направлении он перемещается по пространственно-временному ландшафту. У этого вектора есть имя – вектор скорости в пространстве-времени. Если использовать правильную терминологию, то следует говорить, что этот вектор скорости всегда имеет длину с и может указывать направление только в пределах светового конуса будущего. Световой конус будущего – это причудливое название области, расположенной между двумя очень важными для сохранения причинно-следственных связей линиями, пролегающими под углом 45 градусов. Мы можем полностью описать любой вектор в пространстве-времени, отметив, какая его часть указывает в направлении времени, а какая – в направлении пространства.
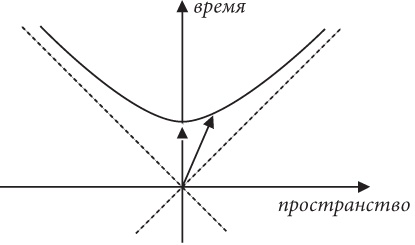
Рис. 9
Мы с вами уже знакомы с положением, что, хотя наблюдатели, которые двигаются с разными скоростями относительно друг друга, по-разному оценивают расстояния во времени и пространстве между двумя событиями, эти расстояния должны меняться таким образом, чтобы расстояние в пространстве-времени всегда оставалось неизменным. Исходя из своеобразной геометрии пространства Минковского это означает, что конец вектора может двигаться по гиперболе, расположенной в пределах светового конуса будущего. В частности, если два события – это лечь спать в десять вечера и проснуться в восемь утра, то находящийся в кровати наблюдатель придет к выводу, что вектор скорости в пространстве-времени направлен вверх по временной оси, как показано на рис. 9, а длина этого вектора – просто количество времени, измеренного по его часам и умноженное на c. Некто, пролетающий мимо на высокой скорости, мог бы воспринять спящего в постели как движущийся объект. В таком случае он включил бы в расчеты еще и движение в пространстве, наблюдая за человеком в постели, а это смещает конец вектора с временной оси. Поскольку длина стрелки не может меняться, ее конец должен оставаться на гиперболе. Эту мысль иллюстрирует вторая, наклонная, стрелка на рис. 9. Как видите, часть вектора, указывающая в направлении времени, увеличилась, а это значит, что с точки зрения быстро движущегося наблюдателя между этими двумя событиями проходит больше времени (другими словами, его часы отсчитывают более десяти часов). Это еще один способ представить странный эффект замедления времени.
Вот и все, что следовало сказать о векторах, – во всяком случае пока (вектор скорости в пространстве-времени понадобится нам снова чуть позже). Несколько следующих абзацев посвящены второму важному фрагменту головоломки E = mc². Представьте себе, что вы физик, пытающийся понять, как устроена Вселенная. Вы уже спокойно воспринимаете идею векторов и даже составили ряд математических уравнений, которые их содержат. А теперь вообразите, что кто-то, скажем один из ваших коллег, говорит вам, что существует особый вектор, который никогда не меняется, что бы ни происходило в той части Вселенной, к которой он относится. Сначала вы, возможно, это проигнорируете: если ничего не меняется, то вряд ли удастся раскрыть суть рассматриваемого вопроса. Но ваш интерес усилится, если коллега уточнит, что этот особый вектор образован посредством суммирования ряда других векторов, каждый из которых связан с отдельной частью объекта, который вы пытаетесь понять. Различные части этого объекта способны перемещаться, и когда они делают это, каждый из отдельных векторов может меняться, но всегда таким образом, что общая сумма всех векторов образует все тот же неизменный особый вектор. Кстати, суммирование векторов – очень легкий процесс, мы еще к нему вернемся.
Чтобы продемонстрировать, насколько полезной может быть идея неизменных векторов, давайте поразмышляем над очень простой задачей: попробуем понять, что происходит с двумя бильярдными шарами в момент их столкновения. Пример из бильярда вряд ли можно назвать жизненно важным, однако физики любят подобные примеры, но не потому, что могут изучать только простые явления или обожают бильярд, а скорее потому, что во многих случаях сложные концепции легче понять, проиллюстрировав их сначала на простых примерах. Но вернемся к бильярду: ваш коллега говорит, что вам следует связать с каждым шаром вектор, который должен быть ориентирован в направлении движения шара. Предполагается, что, сложив два вектора (по одному на каждый шар), можно получить особый неизменный вектор. Это означает, что независимо от того, что происходит в момент столкновения шаров, мы можем быть уверены, что сложение двух векторов, связанных с шарами после столкновения, образует точно такой же вектор, как и полученный из двух шаров до столкновения. Потенциально это очень важный вывод. Наличие особого вектора существенно ограничивает возможные последствия столкновения. Пожалуй, еще большее впечатление произвело бы на нас утверждение вашего коллеги о том, что принцип «сохранения векторов» работает в любой системе событий, происходящих во Вселенной, – от столкновения бильярдных шаров до взрыва звезды. По всей вероятности, для вас не станет неожиданностью тот факт, что физики не используют обозначения «особый вектор», заменив его таким термином, как «вектор импульса», а сохранение векторов широко известно как «закон сохранения импульса».



