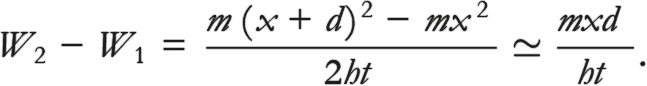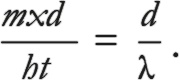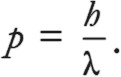Это значит, что вероятность нахождения частицы в точке Х в какое-то более позднее время будет достаточно высокой. Точка Х отличается от других, потому что именно в ней все циферблаты из исходной группы, словно сговорившись, покажут одно и то же время. Но точка Х – не единственная из имеющих особенный характер: все точки слева от Х на расстоянии, равном размеру исходной группы, обладают тем же свойством: циферблаты в них тоже складываются с положительным результатом. Чтобы увидеть это, заметьте, что можно взять циферблат 2 и переместить его в точку на расстоянии d слева от Х. Это будет соответствовать перемещению циферблата на расстояние x, а это то же самое расстояние, на которое мы переместили циферблат 1 по направлению к точке Х. После этого можно переместить циферблат 3 в эту новую точку на расстояние x + d, что будет тем же самым расстоянием, на которое мы до того переместили циферблат 2. Эти два циферблата, следовательно, тоже должны показывать одно и то же время в точке прибытия и суммироваться. Мы можем продолжать делать то же самое для всех циферблатов в исходной группе, но только до тех пор, пока расстояние слева от Х не станет равно размеру исходной группы. За пределами этой особой области циферблаты в основном будут отменять друг друга, потому что останутся без защиты от обычной неконтролируемой квантовой интерференции
[15].
Истолкование этого эксперимента очевидно: группа циферблатов движется, как показывает рис. 5.2.
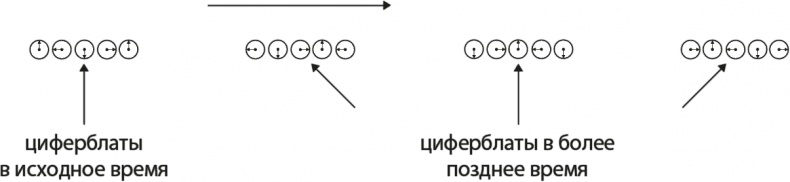
Рис. 5.2. Группа циферблатов с постоянной скоростью движется вправо. Это происходит потому, что в исходной группе стрелки циферблатов повернуты по отношению друг к другу так, как описано в тексте
Это удивительный результат. Задав начальную группу с помощью часов, показывающих разное, а не одинаковое время, мы пришли к описанию движущейся частицы. Интересно, что мы можем установить очень важную связь между часами со сдвинутыми стрелками и поведением волн.
Помните, что в главе 2 нам пришлось ввести идею циферблатов, чтобы объяснить волновое поведение частиц в двухщелевом эксперименте. Вернемся к
рис. 3.3, где мы изобразили набор циферблатов, описывающий волну. Он напоминает набор циферблатов в нашей движущейся группе. Соответствующую волну мы изобразили под группой циферблатов на рис. 5.1, пользуясь совершенно теми же методами, что и ранее: 12 часов – пик волны, 6 часов – ее минимум, а 3 и 9 часов соответствуют нулевой высоте волны.
Как мы могли предвидеть, представление движущейся частицы, видимо, имеет что-то общее с волной. У волны есть длина, соответствующая расстоянию между циферблатами с идентичными показаниями стрелок. Мы изобразили ее на рисунке, обозначив буквой λ.
Сейчас можно вычислить, насколько далеко точка Х должна располагаться от исходной группы, чтобы смежные циферблаты складывались с положительным значением. Это приводит нас к еще одному очень важному результату в квантовой механике и существенно проясняет связь между квантовыми частицами и волнами. Снова наступает момент, когда нам потребуется немного математики.
В первую очередь нужно вывести дополнительную величину, на которую повернута стрелка циферблата 2 по сравнению с циферблатом 1, поскольку дальше циферблат отправится в точку Х. С помощью результатов из начала главы находим, что
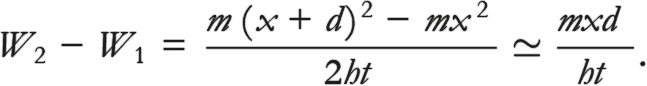
Вы можете сами произвести вычисления, раскрыв скобки и отбросив величину d², поскольку d – расстояние между циферблатами, которое слишком мало по сравнению с x – расстоянием до точки Х, лежащей очень далеко от исходной области.
Довольно несложно записать критерий и для циферблатов, показывающих одно и то же время; нам нужно еще немного подвести стрелки, чтобы при продвижении циферблата 2 это исходное смещение показаний часов полностью компенсировало дополнительный поворот стрелки в ходе перемещения циферблата. Для примера, показанного на рис. 5.1, циферблат 2 дополнительно переводится на ¼, потому что мы должны будем повернуть стрелку на четверть часа вперед. Точно так же циферблат 3 подводится на ½, потому что мы должны будем повернуть стрелку вперед на полчаса. Символически выразить долю полного оборота в виде d / λ, где d – расстояние между циферблатами, а λ – длина волны.
Если вы этого пока не улавливаете, рассмотрите случай, при котором расстояние между двумя циферблатами будет равняться длине волны. Тогда d = λ, а, следовательно, d / λ = 1, что соответствует одному полному обороту, при этом оба циферблата покажут одинаковое время.
Подытожим: чтобы два соседних циферблата показывали в точке Х одинаковое время, требуется, чтобы дополнительный поворот часовой стрелки в начальном положении равнялся дополнительному повороту часовой стрелки при распространении волны на расстояние:
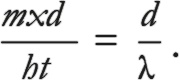
Как и выше, можем упростить это выражение, отметив, что mx / t – это импульс частицы, p. После небольших преобразований уравнения получим:
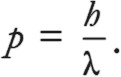
Полученный результат настолько важен, что заслуживает собственного имени. И действительно, эта формула называется уравнением де Бройля, поскольку впервые в сентябре 1923 года ее предложил французский физик Луи де Бройль. Важность формулы в том, что она связывает длину волны с известным импульсом частицы. Иными словами, так проявляется тесная связь между свойством, обычно присутствующим у частиц – импульсом, и свойством, чаще всего ассоциирующимся с волнами, – длиной волны. Таким образом, из наших манипуляций с часами возник корпускулярно-волновой дуализм квантовой механики.
Уравнение де Бройля ознаменовало огромный концептуальный скачок. В своей оригинальной работе он писал, что «воображаемая связанная волна» должна приписываться всем частицам, в том числе электронам, и что поток электронов, проходя через щель, «должен демонстрировать феномен дифракции»
[16]. В 1923 году это были еще теоретические рассуждения, потому что Дэвиссон и Джермер обнаружили появление интерференционной фигуры при испускании пучков электронов только в 1927-м. Эйнштейн сделал примерно то же предположение, что и де Бройль, на других основаниях и приблизительно в это же время. Эти два теоретических результата стали катализатором для развития волновой механики Шрёдингера. В работе, вслед за которой Шрёдингер уже опубликовал уравнение своего имени, он писал: «Нам приходится серьезно отнестись к волновой теории де Бройля – Эйнштейна о движении частиц».