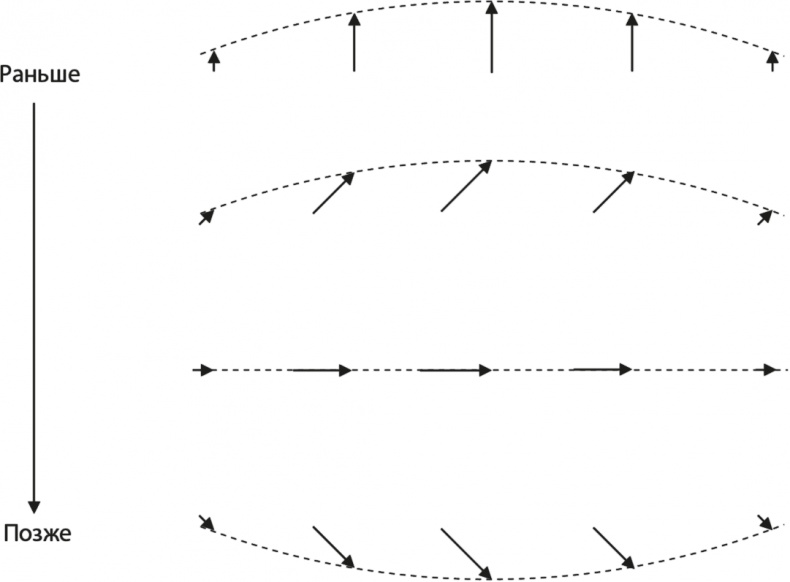
Рис. 6.6. Четыре снимка стоячей волны в последовательные моменты времени. Стрелки на рисунке соответствуют стрелкам часов, а пунктирная линия – проекции «двенадцатичасового» направления. Все стрелки движутся в унисон
Итак, мы выяснили, что удерживаемый электрон описывается набором циферблатов, все стрелки которых вращаются с одинаковой скоростью. Физики, впрочем, обычно так не говорят, а уж музыканты и подавно; те и другие говорят, что стоячие волны – это волны определенной частоты
[28]. Высокочастотные волны соответствуют часам, стрелки которых вращаются быстрее, чем стрелки часов низкочастотных волн. Это понятно, потому что если стрелка часов вращается быстрее, то уменьшается время падения волны с максимума до минимума и обратного подъема (представленного полным оборотом стрелки). Если говорить о водяных волнах, то высокочастотные стоячие волны поднимаются и опускаются быстрее, чем низкочастотные. В музыке говорят, что среднее до имеет частоту 262 Гц, то есть гитарная струна ежесекундно колеблется 262 раза. Нота ля выше среднего до, она имеет частоту 440 Гц, то есть колеблется быстрее (это общепринятый стандарт настройки в большинстве оркестров и для музыкальных инструментов во всем мире). Как мы уже отметили, однако, лишь для чистых синусоид верно, что волны определенной частоты имеют и определенную длину волны. В общем же случае частота – фундаментальная величина, которая описывает стоячие волны, но это определение, кажется, ничего не определяет. Вот вопрос на миллион долларов: что такое электрон определенной частоты? Напомним, что состояния электрона нам интересны, потому что они квантованы, и еще потому, что электрон в одном подобном состоянии остается таким все время (пока нечто не войдет в область потенциала, воздействуя на этот электрон).
Последнее предложение намекает, что мы должны понять значение частоты. В этой главе мы уже встречались с законом сохранения энергии, и это один из самых несомненных законов физики. Сохранение энергии означает, что если электрон в атоме водорода (или в прямоугольной яме) обладает определенной энергией, то эта энергия не может измениться, пока «что-то не произойдет». Иными словами, электрон не может спонтанно изменить свою энергию без какой-либо причины. Кажется, что это не очень интересно, но сравните это со случаем, когда известно, что электрон находится в определенной точке. Как мы все хорошо знаем, он теперь будет перемещаться по всей Вселенной в долю секунды, переводя бесконечное число циферблатов. Но поведение циферблатов для стоячей волны будет иным. Структура циферблатов сохранит свою форму, и все стрелки будут счастливо вращаться, пока что-либо не нарушит их хода. Неизменная природа стоячих волн, таким образом, делает их очевидным кандидатом на описание электрона с определенной энергией.
Сделав шаг, связывающий частоту стоячей волны с энергией частицы, теперь мы можем использовать наше представление о гитарных струнах и предположить, что более высокие частоты должны соответствовать большим энергиям. Дело в том, что высокая частота подразумевает меньшую длину волны (поскольку короткие струны вибрируют быстрее), и мы, изучив конкретный случай прямоугольной потенциальной ямы, можем ожидать, что более короткая длина волны соответствует частице с большей энергией – по уравнению де Бройля. Таким образом, можно сделать важный вывод, который необходимо запомнить: стоячие волны описывают частицы с определенной энергией, и чем больше энергия, тем быстрее идут стрелки часов.
Резюмируем: если электрон удерживается потенциалом, то его энергия квантуется. На физическом жаргоне это звучит так: удерживаемый электрон может существовать только на определенных «энергетических уровнях». Минимально возможная энергия электрона соответствует его описанию только одной стоячей волной «основного тона»
[29], и этот энергетический уровень обычно называют основным состоянием. Энергетические уровни, соответствующие стоячим волнам с более высокими частотами, носят название возбужденных состояний.
Представим электрон с определенной энергией, удерживаемый в прямоугольной потенциальной яме. Мы говорим, что он «находится на определенном энергетическом уровне» и его квантовая волна связана с единственным значением n. Выражение «находится на определенном энергетическом уровне» отражает тот факт, что электрон в отсутствие любых внешних влияний не делает ничего. Обобщим: электрон можно описать сразу многими стоячими волнами, как звук гитары состоит из многих гармоник. Это значит, что в общем случае электрон не имеет конкретной энергии.
Важно, что при измерении энергии электрона всегда будет получаться величина, равная той, которая связана с одной из составляющих стоячих волн. Чтобы вычислить вероятность нахождения электрона с конкретной энергией, мы должны взять циферблаты, связанные с конкретной составляющей общей волновой функции, возвести их в квадрат и сложить. От получившегося числа и зависит вероятность нахождения электрона в этом конкретном энергетическом состоянии. Сумму всех таких вероятностей (одна для каждой составляющей стоячей волны) должна в итоге получиться равной единице, и это лучшая иллюстрация того, что энергия частицы всегда будет соответствовать конкретной стоячей волне.
Сразу скажем, что электрон может одновременно иметь несколько различных энергий, и это утверждение ничуть не менее странное, чем то, что он имеет множество положений. Конечно, дочитав книгу до этого момента, стресс вы вряд ли испытаете, но для нашего повседневного восприятия это все равно шок. Заметьте, что есть критически важная разница между удерживаемой квантовой частицей и стоячими волнами в бассейне или на гитарной струне. Идея квантования волны на гитарной струне вовсе не странна, потому что волна, которая, собственно, описывает вибрирующую струну, одновременно состоит из многих разных стоячих волн, и все они физически составляют общую энергию волны. Так как смешивать их можно любым образом, действительная энергия вибрирующей струны может принимать вообще любое значение. Однако для электрона, запертого внутри атома, относительный вклад каждой стоячей волны описывает вероятность того, что электрон будет обнаружен с некой конкретной энергией.
Важная разница в том, что водяные волны – это волны водяных молекул, а электронные волны – это определенно не волны электронов.
Все это показывает, что энергия электрона внутри атома квантуется. Это значит, что электрон просто не может иметь энергию, значение которой будет располагаться между определенными разрешенными величинами: примерно как если бы мы сказали, что машина может ехать со скоростью 10 или 40 км/ч, но не с какой-то скоростью между этими двумя величинами. И это фантастически странное умозаключение непосредственно объясняет, почему атомы не испускают свет постоянно, что сопровождалось бы спиральным движением электрона к ядру. Дело в том, что электрон не может постоянно, по чуть-чуть излучать энергию. Единственный способ, которым он может испускать энергию, – потерять ее сразу и полностью.



