То, что мы уже усвоили, можно применить к наблюдаемым свойствам атомов, а именно к уникальному цвету их излучения. На рис. 6.7 показан видимый свет, испускаемый простейшим атомом – водородом. Свет состоит из пяти отчетливых цветов: ярко-красная линия соответствует свету с длиной волны 656 нм, светло-голубая – длине волны 486 нм, а три остальные фиолетовые затухают в ультрафиолетовой части спектра. Эта серия цветных линий известна как серия Бальмера (в честь швейцарского физика и математика Иоганна Бальмера, который в 1885 году предложил формулу для ее описания).

Рис. 6.7. Водородная серия Бальмера: вот что видно, когда свет, испускаемый газообразным водородом, проходит через спектроскоп
Бальмер понятия не имел, почему его формула верна, потому что квантовая теория еще не была открыта: он просто выразил регулярность серии удобной математической формулой. Но мы можем пойти дальше и показать, что все дело в разрешенных квантовых волнах внутри атома водорода.
Мы знаем, что свет можно представить в виде потока фотонов, каждый из которых обладает энергией E = hc / λ, где λ – длина световой волны
[30]. Таким образом, то, что атомы испускают свет лишь определенного цвета, означает, что они испускают фотоны с четко определенной энергией. Мы выяснили также, что электрон, «заключенный в атоме», может обладать лишь определенной конкретной энергией. Это небольшой шаг на пути к объяснению давней загадки цвета излучения атомов: разные цвета соответствуют испусканию фотонов, при котором электроны «перепрыгивают» с одного разрешенного энергетического уровня на другой. Эта идея подразумевает, что наблюдаемая энергия фотона всегда должна соответствовать разнице между парой разрешенных значений энергии электрона. Такой способ описания физических явлений отлично иллюстрирует ценность выражения состояния электрона в терминах разрешенных значений его энергии. Если вместо этого мы бы предпочли говорить о разрешенных значениях импульса электрона, то квантовая природа этих явлений не была бы столь очевидной и нам не удалось бы с такой легкостью заключить, что атом может испускать и поглощать излучение только с определенными длинами волны.
Модель атома как частицы в ящике недостаточно точна для того, чтобы позволить нам вычислить значения энергии электрона в реальном атоме, необходимые для проверки всей нашей идеи. Но можно провести достаточно точные вычисления, если мы лучше смоделируем потенциал вблизи протона, который и удерживает электрон. Достаточно сказать, что эти вычисления без тени сомнения подтверждают: здесь-то и кроется причина появления загадочных спектральных линий.
Наверное, вы заметили, что мы пока не объяснили, почему электрон, испуская фотон, теряет энергию. Для целей, обсуждающихся в этой главе, такое объяснение не требуется. Но что-то должно побудить электрон покинуть святилище стоячей волны, и это «что-то» будет темой главы 10. Сейчас же просто скажем: чтобы объяснить наблюдаемые спектры светового излучения, испускаемого атомами, необходимо предположить, что свет испускается, когда электрон перескакивает с одного энергетического уровня на другой, с меньшей энергией. Разрешенные энергетические уровни определяются формой удерживающего ящика и варьируются от атома к атому, потому что разные атомы служат разной средой, внутри которой заключены их электроны.
До настоящего времени мы сполна использовали возможности для объяснения положения дел с помощью очень простой картины атома, но вообще-то не так уж верно считать, что электроны свободно передвигаются внутри какого-то ящика, который их ограничивает. Они передвигаются вблизи множества протонов и других электронов, и для лучшего понимания природы атомов мы должны определить, как более точно описать эту среду.
Атомный ящик
Вооружившись понятием потенциала, можно более точно описать атомы. Начнем с простейшего из всех – атома водорода. Он состоит всего из двух частиц – электрона и протона. Протон почти в 2000 раз тяжелее электрона, так что мы можем предположить, что он почти ничего не делает и просто покоится на месте, создавая потенциал, удерживающий электрон.
Протон обладает положительным электрическим зарядом, а электрон – равным ему отрицательным зарядом. Кстати, причина, по которой электрические заряды протона и электрона в точности равны и противоположны друг другу, – это одна из величайших загадок физики. Вероятно, есть очень веская причина, которая связана с некоей пока еще не открытой теорией субатомных частиц, но на момент написания этой книги никто не может сказать этого с уверенностью.
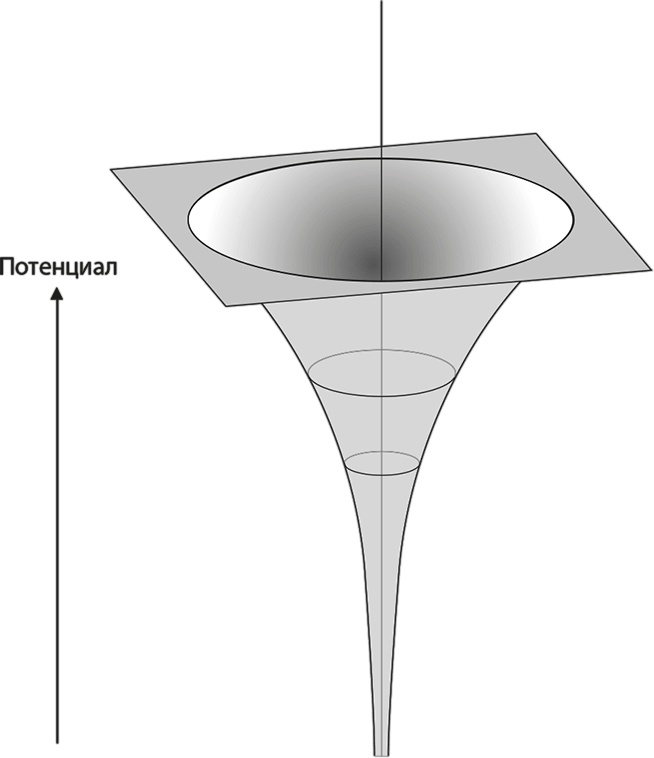
Рис. 6.8. Потенциальная яма Кулона вокруг протона. Яма глубже всего там, где находится сам протон
Что мы действительно знаем, так это то, что противоположные заряды притягиваются и протон перетягивает электрон к себе, поэтому, с точки зрения доквантовой физики, он может притянуть к себе электроны на сколь угодно малое расстояние. Насколько оно мало, зависит от конкретной природы протона: он твердый шарик или какое-то облако? Но этот вопрос не имеет физического смысла, потому что, как мы уже видели, существует минимальный энергетический уровень, на котором может находиться электрон и который определяется (грубо говоря) квантовой волной самой большой длины, которая способна поместиться в потенциал, созданный протоном. Этот созданный протоном потенциал мы изобразили на рис. 6.8. Глубокая «яма» функционирует так же, как уже известная нам прямоугольная потенциальная яма, только ее форма уже не столь проста. Она носит название потенциала Кулона, потому что подчиняется закону, описывающему взаимодействие двух электрических зарядов, который впервые вывел Шарль Огюстен де Кулон в 1783 году.
Проблема, однако, остается той же самой: мы должны выяснить, какие квантовые волны могут соответствовать этому потенциалу, что и определит разрешенные энергетические уровни атома водорода. Будучи бесхитростными, мы могли бы сказать, что это делается посредством «решения волнового уравнения Шрёдингера для потенциальной ямы Кулона», что служит способом применения правила перевода циферблатов. Детали этого процесса чисто технические, даже для таких простых объектов, как атом водорода. К счастью, мы не узнаем здесь почти ничего нового по сравнению с тем, что уже усвоили, так что перейдем прямо к ответу. Рис. 6.9 показывает некоторые получающиеся стоячие волны для электрона в атоме водорода. Это картина распределения вероятностей нахождения электрона в какой-либо точке. В более светлых областях такая вероятность выше. Конечно, реальный атом водорода трехмерный, и эти рисунки соответствуют разрезам в центре атома. Рисунок слева вверху – это волновая функция основного состояния, показывающая, что электрон в этом случае обычно находится на расстоянии примерно 1 × 10–10 м от протона. Энергия стоячих волн нарастает от левого верхнего к правому нижнему рисунку. Масштаб тоже изменяется в восемь раз от левого верхнего к правому нижнему рисунку, так что светлая область, покрывающая большую часть левого верхнего рисунка, имеет примерно тот же размер, что и маленькие яркие точки в центре двух правых рисунков. Это значит, что электрон, скорее всего, будет располагаться дальше от протона, когда он находится на более высоких энергетических уровнях (а следовательно, слабее с ним связан). Ясно, что эти волны совсем не синусоиды, то есть не соотносятся с состояниями определенного импульса. Но, как мы изо всех сил стараемся подчеркнуть, они соответствуют состояниям определенной энергии.




