Очевидно, что размер нашего кубика и его расположение внутри звезды совершенно произвольны, поэтому никакие выводы о самой звезде не могут зависеть от этих деталей. Начнем с того, что сделаем нечто совершенно бесполезное на первый взгляд.
Мы имеем возможность выразить размер и местонахождение нашего куба через размер всей звезды. Если R – радиус звезды, можно записать расстояние куба от центра звезды как r = aR, где a – просто безразмерное число между 0 и 1. Под безразмерностью мы понимаем то, что оно не соответствует никакой единице, это только численный показатель. Если a = 1, то куб находится на поверхности звезды, а если a = ½, куб расположен строго посередине. Точно так же можно выразить размер куба через радиус звезды. Если L – длина стороны куба, мы можем записать L = bR, где b – это опять же только численный показатель, который должен быть очень мал, если наш куб мал относительно звезды. Здесь нет абсолютно ничего сложного, так что на этом этапе все должно казаться настолько простым, что записывать, кажется, даже бесполезно.
Заметим только, что использовать расстояние R совершенно естественно, потому что нет других относящихся к белому карлику расстояний, которые могли бы представлять сколь-нибудь разумную альтернативу.
Мы можем продолжать свои «бессмысленные» занятия и выразить плотность звезды в месте нахождения куба через среднюю плотность звезды. Запишем, что ρ = fρ̅, где f – опять же просто численный показатель, а ρ̅ – средняя плотность звезды. Как мы уже указывали, плотность куба зависит от его положения внутри звезды – чем ближе к центру, тем больше плотность. Так как средняя плотность ρ̅ от положения куба не зависит, зависимость должен обнаруживать показатель f, который, таким образом, зависит от расстояния r, а следовательно, и от произведения aR. И это ключевая информация, лежащая в основе всех наших последующих вычислений: f – это чистое число, а R – не чистое число, а результат измерения расстояния. И f может зависеть только от a, а никак не от R. Это очень важный результат, потому что он свидетельствует, что плотность белого карлика «не зависит от масштаба». Это значит, что плотность изменяется на радиусе независимо от величины этого радиуса. Например, плотность в точке, расположенной на ¾ расстояния от центра до поверхности звезды, будет совершенно одинаковой в любом белом карлике независимо от его размера. Есть два способа оценки этого исключительно важного результата, и мы решили, что приведем здесь оба. Один из нас объясняет это так: «Дело в том, что любая безразмерная функция от r (а f – это именно она) может быть только безразмерной, так как это функция безразмерной переменной, а единственная безразмерная переменная в нашем случае – это r / R = a, поскольку R – единственная величина, связанная с расстоянием, из находящихся в нашем распоряжении».
Второй соавтор считает более четким следующее разъяснение: «f может в принципе по-разному сложным образом зависеть от r – расстояния кубика от центра звезды. Но давайте представим, что эти величины прямо пропорциональны, то есть f ∝ r. Иными словами, f = Br, где B – константа. Здесь самое важное то, что f – чисто численный показатель, в то время как r измеряется, например, в метрах. Отсюда следует, что B должно измеряться в 1/м, чтобы единицы расстояния взаимно сокращались. Итак, что нужно выбрать для B? Мы не можем назначить нечто произвольное, например «1 обратный метр», поскольку это бессмысленно и никак не связано со звездой. Почему, например, не выбрать один обратный световой год, получив совершенно другой ответ? Единственное расстояние, с которым мы имеем дело, – это R, физический радиус звезды, так что придется использовать его, чтобы f всегда оставалось чистым числом. Это значит, что f может зависеть только от r / R. Вы, наверное, уже поняли, что тот же вывод можно было сделать, если бы мы начали с предположения, что, например, f ∝ r²». Собственно, ровно то же говорил и первый соавтор, только сейчас вышло длиннее.
Это значит, что можно выразить массу нашего кубика размером L и объемом L³, находящегося на расстоянии r от центра звезды, в виде Mcube = f(a)L³ρ̅. Мы написали f(a), а не просто f, чтобы не забывать, что f на деле зависит от нашего выбора a = r / R, а не от каких-то масштабных свойств звезды. Тот же аргумент можно использовать при указании, что мы можем записать Min = g(a)M, где g(a) – это опять же только функция от a. Например, функция g(a), высчитанная для a = ½, подсказывает, какое количество массы звезды приходится на сферу с радиусом, равным половине радиуса всей звезды, и это количество неизменно для всех белых карликов независимо от их радиуса по причине, приведенной в предыдущем абзаце
[61]. Вы могли заметить, что мы постоянно избавляемся от тех символов, которые встречаются в уравнении (1), заменяя их безразмерными величинами (a, b, f и g), помноженными на величины, зависящие только от массы и радиуса звезды (средняя плотность звезды определяется через M и R, поскольку ρ̅ = M / V и V = 4πR³ / 3, объем сферы). В довершение нужно сделать то же самое для разницы давлений, которую мы благодаря уравнению (4) можем записать как Pbottom – Ptop = = h(a, b)κρ̅5/3, где h(a, b) – безразмерная величина. То, что h(a, b) зависит одновременно от a и b, связано с тем, что разница давлений зависит не только от местоположения куба (представленного a), но и от его объема (представленного b): у более крупных кубов больше разница давлений. Самое важное здесь то, что, как и f(a), и g(a), h(a, b) не может зависеть от радиуса звезды.
Мы можем воспользоваться только что выведенными выражениями и переписать уравнение (1):
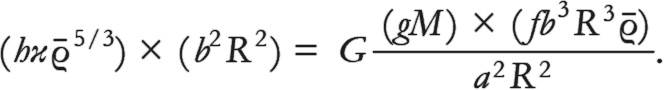
Кажется, что в уравнении царит хаос; непохоже, чтобы уже на следующей странице мы пришли к результату. Главное – заметить, что уравнение выражает отношения между массой звезды и ее радиусом – конкретная зависимость между ними уже нащупывается (или на виду, но чудовищно далека – в зависимости от вашего уровня владения математикой). После введения в наше хаотическое уравнение средней плотности звезды (то есть ρ̅ = M / (4πR³ / 3)) оно принимает следующий вид: