Для начала предположим, что элементарные строительные кирпичики природы – это частицы. Это подтверждается не только двухщелевым экспериментом, в котором электроны всегда прибывают в конкретные места экрана, но и множеством других исследований. И действительно, «физика частиц» не зря так называется. Нужно решить следующий вопрос: как перемещаются частицы? Конечно, проще всего предположить, что они двигаются по идеально прямым линиям или же по кривым, если на них действуют силы согласно законам Ньютона. Однако это не может быть верным, потому что любое объяснение двухщелевого эксперимента предполагает, что электроны «интерферируют друг с другом», проходя через щели, а для этого они должны каким-то образом рассеиваться. Итак, проблема – создать такую теорию точечных частиц, чтобы эти частицы еще и рассеивались. Но задача не так нереальна, как кажется: это можно сделать, если «позволить» каждой частице находиться одновременно в нескольких местах. Конечно, это опять-таки кажется невозможным, но предположение о том, что частица может находиться в нескольких местах одновременно, по крайней мере, довольно ясное, даже если звучит весьма глупо. С этого момента мы будем называть такие частицы – противоречащие интуиции, рассеянные, но при этом точечные – квантовыми.
Высказав предположение, что «частица может одновременно находиться более чем в одном месте», мы отрываемся от повседневного опыта и вступаем на неизведанную территорию. Одно из главных препятствий для развития понимания квантовой физики – смятение, порождаемое таким способом мышления. Чтобы его избежать, нужно следовать за Гейзенбергом и учиться спокойно мириться с взглядами на мир, идущими вразрез с житейским опытом. «Неудобство» теории часто ошибочно принимается за смятение, и нередко изучающие квантовую физику продолжают пытаться понять происходящее с точки зрения повседневного опыта. Но к смятению ведет сопротивление новым идеям, а не внутренняя сложность самих идей, потому что реальный мир попросту устроен не так, как подсказывает нам повседневный опыт. И поэтому нужно подходить к делу с непредубежденным умом и не смущаться кажущейся странностью. Это понимал даже Шекспир – его Гамлет говорит: «Как к чудесам, вы к ним и отнеситесь. Гораций, много в мире есть того, что вашей философии не снилось»
[5].
Хороший способ начать – тщательно поразмыслить над версией двухщелевого эксперимента для волн воды. Наша цель – выяснить, что же в волнах вызывает появление интерференционной фигуры. Мы должны убедиться, что теория квантовых частиц включает такое же поведение и мы сможем попытаться объяснить двухщелевой эксперимент и для электронов.
Волны, проходящие через две щели, могут интерферировать друг с другом по двум причинам. Первая: волна проходит через обе щели одновременно, создавая две новые волны, которые отклоняются и смешиваются. Очевидно, что волна может себя так вести. У нас нет ни малейших проблем с тем, чтобы представить себе одну длинную океанскую волну, которая накатывает на берег и разбивается о пляж. Это стена воды – распростертая, не стоящая на месте. Таким образом, надо понять, как сделать такой же «распростертой, не стоящей на месте» нашу частицу. Вторая причина в том, что две новые волны, отходящие от щелей, могут при смешивании либо добавляться друг к другу, либо ослаблять действие друг друга. Эта способность двух волн интерферировать, очевидно, и будет ключевой для объяснения появления интерференционной фигуры. Крайний случай – совпадение максимума одной волны с минимумом другой. В этом случае они полностью погасят друг друга. Поэтому мы сталкиваемся с необходимостью заставить нашу квантовую частицу каким-то образом интерферировать саму с собой.
Двухщелевой эксперимент связывает поведение электронов с поведением волн, поэтому давайте посмотрим, насколько далеко может зайти это соответствие. Посмотрим на рис. 3.1, сначала проигнорировав линии, соединяющие точки А с Е и B с F, и соcредоточимся на волнах.
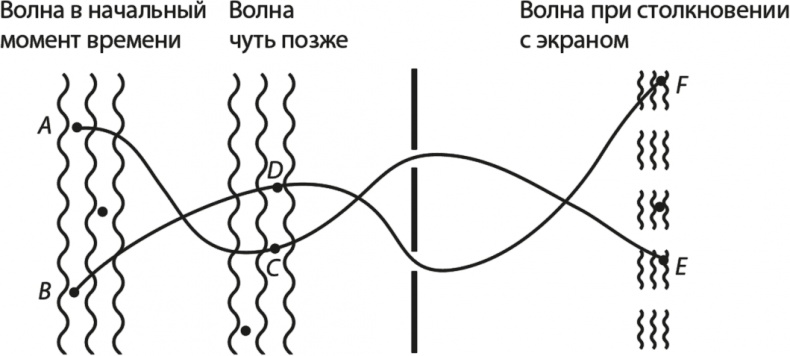
Рис. 3.1. Как волна, описывающая поведение электрона, движется от источника к экрану и как ее нужно интерпретировать в качестве представления всех вариантов траекторий электрона. Пути от A до C и E и от B до D и F иллюстрируют всего лишь две из бесконечного множества траекторий, по которым может двигаться одиночный электрон
Наш рисунок может описывать цистерну с водой. Тогда волнистые линии представляют – слева направо – то, как водяная волна катится через цистерну. Допустим, мы сфотографировали цистерну сразу после того, как деревянная доска слева ударила по воде, вызвав волну. На фотографии будет видна новообразованная волна, простирающаяся сверху вниз. Вся остальная вода в цистерне остается спокойной. На второй фотографии, сделанной чуть позже, видно, как водяная волна двигается к щелям, оставляя за собой ровную поверхность. Еще позже волна проходит через пару щелей и создает полосатую интерференционную фигуру, которую иллюстрируют волнистые линии в правом углу.
А сейчас давайте перечитаем последний абзац, только вместо «водяной волны» подставим «электронную волну», что бы это ни значило. Электронная волна, если ее интерпретировать должным образом, может объяснить ту полосатую фигуру, которую мы хотим понять, потому что в эксперименте она ведет себя так же, как волна воды. Но осталось объяснить, почему же электронная фигура получается из точек, когда электроны попадают на экран один за другим. На первый взгляд, это противоречит идее гладкой волны, но на самом деле это не так. Нужно догадаться, что мы можем предложить следующее объяснение: электронную волну следует интерпретировать не как реальное материальное возмущение (как в случае с волной воды), а как некий способ информирования нас о том, где, вероятно, электрон будет обнаружен. Заметьте, мы говорим «электрон», а не «электроны», потому что волна должна описать поведение одиночного электрона – таким образом мы получим возможность объяснить, откуда же берутся эти точки. Это электронная волна, а не волна электронов, и тут нельзя ошибаться. Если мы представим себе снимок волны в какой-то момент времени, то возникнет мысль интерпретировать его следующим образом: там, где волна наибольшая, существует наибольшая вероятность найти электрон, а там, где волна меньше всего, вероятность встретить наш электрон наименьшая. Когда волна наконец достигает экрана, там появляется маленькая точка, которая и сообщает о его местонахождении. Единственная задача электронной волны – дать нам возможность вычислить шансы на то, что электрон попадет в определенную точку экрана. Если же не беспокоиться, чем в действительности «является» электронная волна, то все сразу становится ясным, потому что как только мы рассчитаем волну, то сразу сможем сказать, где, скорее всего, располагается электрон. Самое интересное начинается позже, когда мы пытаемся понять, как связано наше предположение по поводу электронной волны с путешествием электрона от щели к экрану.



