Сравнение с двумя подходящими друг к другу элементами головоломки выбрано не случайно. Вспомним, что в основе трудов Римана и Эйнштейна лежит метрический тензор, т. е. набор из десяти величин, определяющих каждую точку в пространстве. Это естественное обобщение фарадеевой концепции поля. На рис. 2.3 мы видели, как эти десять величин можно расположить на условной шахматной доске с полем 4×4. Обозначим эти десять величин как g11, g12 и т. д. Далее, поле Максвелла — совокупность четырёх величин для каждой точки пространства. Эти четыре величины можно обозначить как А1, А2, А3, А4.
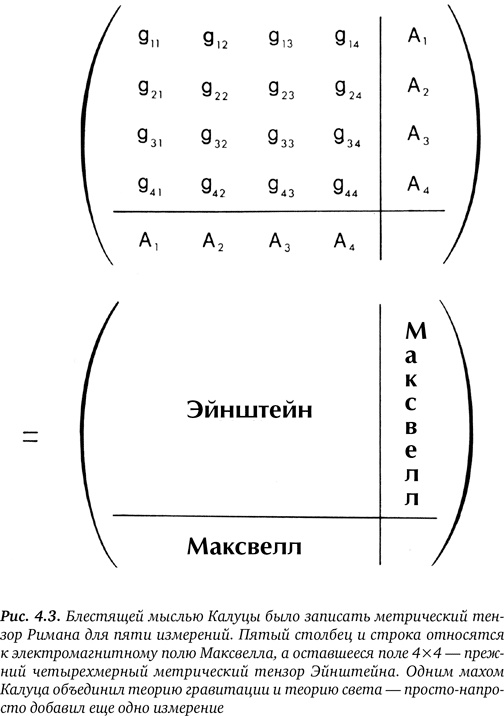
Для того чтобы понять смысл фокуса Калуцы, начнём с римановой теории в пяти измерениях. В этом случае метрический тензор будет представлять собой подобие шахматной доски с полем 5×5. По определению переименуем компоненты поля Калуцы, чтобы часть стала элементами исходного поля Эйнштейна, часть — элементами поля Максвелла (рис. 4.3). В этом и заключается суть фокуса Калуцы, который стал для Эйнштейна полной неожиданностью. Просто дополнив полем Максвелла поле Эйнштейна, Калуца сумел собрать из них пятимерное поле.
Отметим, что 15 компонентов пятимерного гравитационного поля Римана достаточно, чтобы вместить десять компонентов поля Эйнштейна и четыре компонента поля Максвелла! Таким образом, блестящую мысль Калуцы можно в примитивном виде записать так:
(оставшийся компонент — скалярная частица, не играющая роли в нашей дискуссии). При тщательном анализе полной пятимерной теории обнаруживается, что поле Максвелла прекрасно встраивается в метрический тензор Римана, как и утверждал Калуца. Таким образом, элементарное с виду уравнение является выражением одной из наиболее основополагающих идей века.
Словом, пятимерный метрический тензор содержит и поле Максвелла, и метрический тензор Эйнштейна. Эйнштейну не верилось, что такая простая идея способна дать объяснение двум наиболее фундаментальным силам природы — гравитации и свету.
Что же это — салонный фокус? Чудеса нумерологии? Или чёрная магия? Эйнштейн, глубоко потрясённый письмом Калуцы, поначалу не хотел отвечать на него. Над этим письмом он размышлял два года — на редкость длинный срок для решения вопроса о публикации важной статьи. Наконец, убедившись в её потенциальной значимости, Эйнштейн представил статью для публикации в числе трудов Прусской академии наук. Статья имела внушительный заголовок — «Проблема единства физики».
В истории физики ещё никому не удавалось найти хоть какое-нибудь применение четвёртому измерению. Со времён Римана было известно, что математика многомерности поразительно красива, но для физики совершенно бесполезна. И вот теперь впервые применение четвёртому пространственному измерению было найдено, да ещё для объединения законов физики! В каком-то смысле Калуца указывал, что четыре измерения Эйнштейна «слишком тесны», чтобы вместить и электромагнитные, и гравитационные силы.
Теперь-то мы видим, что в историческом плане работа Калуцы не была полной неожиданностью. Большинство историков науки, упоминая о трудах Калуцы, заявляют, что идея пятого измерения стала громом среди ясного неба, оказалась абсолютно неожиданной и оригинальной. Физическим исследованиям свойственна преемственность, и эти историки всполошились, обнаружив, что новая научная область для исследований открылась без каких-либо исторических прецедентов. Но их изумление, вероятно, вызвано тем, что они не знакомы с ненаучными трудами мистиков, литераторов, авангардистов. Пристальное рассмотрение культурно-исторических условий указывает на то, что не стоит считать появление труда Калуцы полной неожиданностью. Как мы уже убедились, благодаря Хинтону, Цёлльнеру и другим вероятность существования высших измерений была, по-видимому, наиболее популярной квазинаучной идеей, витающей в мире искусства. Если рассматривать её в более широком культурном контексте, серьёзное отношение кого-нибудь из физиков к общеизвестной идее Хинтона, согласно которой свет — колебания четвёртого измерения, было лишь вопросом времени. В некотором смысле работа Римана оплодотворила мир искусств и литературы с помощью Хинтона и Цёлльнера, а затем, вероятно, произошло обратное опыление мира науки посредством труда Калуцы. (В поддержку этой гипотезы: недавно Фройнд обнаружил, что Калуца предложил пятимерную теорию гравитации не первым. Гуннар Нордстрём, соперник Эйнштейна, опубликовал первую работу, посвящённую пятимерной теории поля, однако она была слишком примитивной, чтобы содержать теории Эйнштейна и Максвелла. Тот факт, что и Калуца, и Нордстрём независимо друг от друга обратились к пятому измерению, указывает, что идеи, витающие в мире популярной культуры, повлияли на их мышление
{40}.)
Пятое измерение
Для каждого физика первая встреча с пятым измерением становится чем-то вроде удара. Питер Фройнд хорошо помнит тот момент, когда он познакомился с пятым и другими высшими измерениями. Это событие произвело на него глубокое и неизгладимое впечатление.
Оно произошло в 1953 г. в Румынии, где родился Фройнд. Смерть Иосифа Сталина снизила напряжённость в обществе. В тот год Фройнд, одарённый ученик колледжа, присутствовал на лекции румынского математика Георге Врэнчану. Фройнд отчётливо вспоминает, как Врэнчану отвечал на важный вопрос: почему свет и гравитация несовместимы друг с другом? Затем лектор упомянул давнюю теорию, содержащую и теорию света, и уравнения гравитации Эйнштейна. Её секрет заключался в применении теории Калуцы — Клейна, сформулированной для пяти измерений.



