Если бы квантовая механика была ошибочной, тогда перестала бы функционировать вся электроника, в том числе телевизоры, компьютеры, радио- и стереоприемники и т. д. (Мало того, если бы квантовая теория была неверна, атомы, из которых состоят наши тела, распались бы, и мы бы мгновенно исчезли. Согласно уравнениям Максвелла электроны, вращающиеся в атоме, должны были бы в пределах микросекунды терять свою энергию и проникать в ядро. Квантовая теория предотвращает это внезапное разрушение. Таким образом, сам факт нашего существования — наглядное свидетельство правильности квантовой механики.)
Кроме того, это означает существование конечной и поддающейся вычислению вероятности того, что «невозможные» события произойдут. Например, я могу подсчитать вероятность того, что неожиданно исчезну, пройду Землю насквозь и вновь возникну на Гавайях. (Следует отметить, что время, которое нам придётся провести в ожидании подобного события, превышает продолжительность существования Вселенной. Так что мы не можем использовать квантовую механику для прокладки туннелей к излюбленным местам отдыха по всему миру.)
Поле Янга — Миллса. Преемники Максвелла
После первого громкого успеха в 1930–1940-х гг., не имеющего прецедентов в истории науки, к 1960-м гг. квантовая физика начала выдыхаться. Мощные ускорители частиц, построенные для разрушения ядра атома, позволили обнаружить среди остатков сотни загадочных частиц. По сути дела, физиков захлестнул бурный поток экспериментальных данных, поступающих из ускорителей.
Если Эйнштейн вывел основы общей теории относительности при помощи одной только интуиции, то в 1960-е гг. специалисты по физике частиц не страдали от нехватки экспериментальных данных. Как признавался Энрико Ферми, один из создателей атомной бомбы, «если бы я был в состоянии запомнить названия всех этих частиц, я стал бы ботаником»
{44}. По мере того как среди обломков разрушенных атомов обнаруживались сотни «элементарных» частиц, специалисты предлагали бесчисленное множество объяснений, связанных с этими частицами, но успеха эти объяснения не имели. Количество неверных гипотез было настолько велико, что даже появилась шутка о периоде полураспада теории субатомной физики, составляющем всего два года.
Когда смотришь на все эти тупиковые пути и неудачные начала физики частиц того периода, невольно вспоминается анекдот про учёного и блоху.
Однажды учёный выдрессировал блоху, чтобы она подпрыгивала при звуке колокольчика. Затем, используя микроскоп, он обездвижил одну лапку блохи и после этого позвонил. Блоха всё равно подпрыгнула.
Учёный обездвижил вторую лапку и опять позвонил. Блоха снова подпрыгнула.
Так учёный раз за разом выводил из строя конечности блохи, но, когда подавал сигнал, всякий раз записывал в журнале наблюдений, что блоха сделала прыжок.
Наконец непарализованной осталась лишь одна блошиная нога. Когда же учёный обездвижил и эту ногу и подал сигнал, к его удивлению, блоха не подпрыгнула.
И учёный торжественно обнародовал вывод, сделанный на основании неопровержимых научных данных: блохи слышат с помощью ног!
Хотя специалисты в области физики высоких энергий часто напоминают учёных из этого анекдота, за несколько десятилетий постепенно начала складываться последовательная квантовая теория вещества. В 1971 г. голландец, аспирант Герард 'т Хоофт, которому в то время было немногим больше двадцати лет, сделал ключевое открытие, способствовавшее единому описанию трёх квантовых сил (за исключением силы тяготения), в итоге изменившее ландшафты теоретической физики.
Опираясь на аналогию с фотонами, квантами света, физики предположили, что слабое и сильное взаимодействия вызвано обменом квантами энергии, получившими название квантов полей Янга — Миллса. Поля Янга — Миллса, которые в 1954 г. открыли Чжэньнин Янг и его ученик Роберт Миллс, представляют собой обобщение поля Максвелла, введённого веком ранее для описания света, с той разницей, что поле Янга — Миллса может быть более многокомпонентным и иметь электрический заряд (фотон электрическим зарядом не обладает). В случае слабого взаимодействия квант, соответствующий полю Янга — Миллса, — это W-частица, которая может иметь заряд, равный +1, 0 или — 1. Для случая сильного взаимодействия квант, соответствующий полю Янга — Миллса, — тот «клей», который удерживает вместе протоны и нейтроны, — был назван глюоном.
Несмотря на то что в целом картина выглядела убедительно, в 1950–1960-е гг. физиков сбивало с толку то, что поле Янга — Миллса не относится к «перенормируемым», т. е. не даёт конечных и значимых величин применительно к простым взаимодействиям. Таким образом, с точки зрения описания слабых и сильных взаимодействий квантовая теория бесполезна. Квантовая физика упёрлась в глухую стену.
Проблема возникла, так как физики, вычисляя, что произойдёт при столкновении двух частиц, пользовались так называемой теорией возмущений, т. е. завуалированным способом указать, что они прибегали к хитроумным приближениям. К примеру, на рис. 5.2, а мы видим, что происходит при столкновении электрона с другой частицей, участвующей в слабом взаимодействии, — неуловимым нейтрино. На первый взгляд, это взаимодействие можно описать диаграммой (она называется «диаграммой Фейнмана»), показывающей, что обмен квантом слабого взаимодействия — W-частицей — происходит между электроном и нейтрино. В первом приближении мы получаем грубое, но приемлемое соответствие экспериментальным данным.
Однако согласно квантовой теории в наше первое приближение следует внести небольшие поправки. Чтобы сделать наши вычисления строгими, надо также добавить к диаграммам Фейнмана все возможные линии, в том числе с «петлями» на них, как на рис. 5.2, б. В идеале эти квантовые поправки должны быть совсем маленькими. Ведь как мы уже упоминали, квантовая теория для того и предназначена, чтобы вносить крохотные квантовые поправки в ньютонову физику. Но, к ужасу учёных, эти квантовые поправки, или «петлевые линии», оказались не маленькими, а бесконечными. Как ни мудрили физики над своими формулами, как ни пытались замаскировать эти бесконечные величины, расхождения упорно обнаруживались при любых вычислениях квантовых поправок.
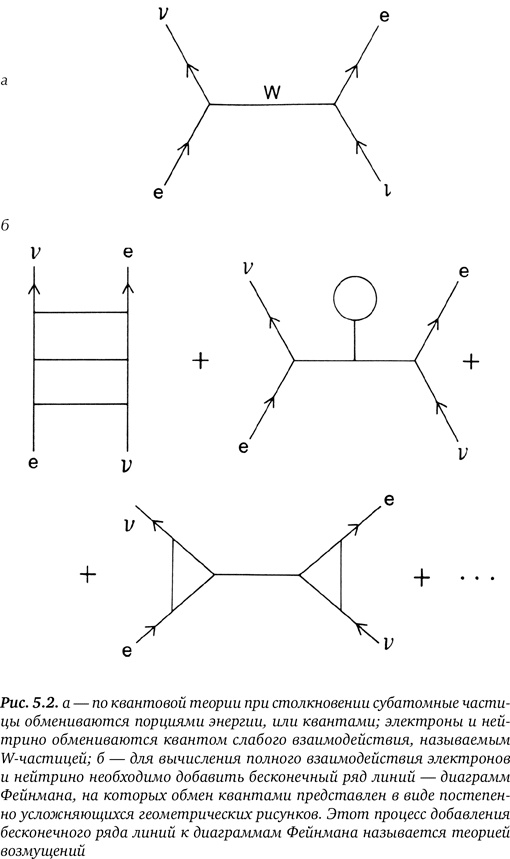
Более того, поле Янга — Миллса приобрело устрашающую репутацию метода, головоломно усложняющего расчёты — в сравнении с более простым полем Максвелла. Согласно мифам, с которыми ассоциируется поле Янга — Миллса, для практических вычислений оно совершенно не подходит ввиду своей сложности. Вероятно, 'т Хоофту просто повезло: будучи аспирантом, он ещё не успел заразиться предубеждениями маститых физиков. Пользуясь методами, которые первым описал его научный руководитель Мартинус Велтман, 'т Хоофт доказал: всякий раз, когда мы сталкиваемся с «нарушением симметрии» (о нём мы поговорим далее), поле Янга — Миллса приобретает массу, но остаётся конечной теорией. 'т Хоофт продемонстрировал, что благодаря графам с петлями можно не рассматривать бесконечности или нивелировать их влияние.



