С произвольностью в этой области было покончено: меры больше не могут основываться на длине блохи или размере человеческого шага, но должны исходить из универсального природного феномена. Политическое и метрологическое равенство, связь науки и политики, без всякого сомнения, не была случайной.

Одна из 16 пластин эталона метра, представленная Бюро мер и весов города Парижа.
Научная революция
Революция мобилизовала ученых и сделала их участниками бурных политических событий: астроном Байи, геометры Кондорсе, Монж и Лаплас, инженер Карно, химики Лавуазье, Фуркруа и Бертолле... Некоторые научные философы и историки считают, что связь между наукой и революцией неслучайна и политики и ученые, каждый в своей области, применяют одинаковые принципы. Как газ представляет собой совокупность молекул или живой организм — совокупность клеток, так государство рассматривается в качестве совокупности граждан, составляющих нацию. Уже прошли те времена, когда Людовик XIV, «король-солнце», восклицал: «Государство — это я!»
Тогда же состоялось и рождение шкалы Цельсия: было решено использовать метрическую систему и для измерения температуры. Один градус Цельсия представляет собой сотую долю температуры, необходимую для прохождения от точки замерзания воды до точки ее кипения. Однако окончательный эталон еще не был утвержден — все ожидали возвращения ученых, которые должны были измерить дугу меридиана и четко определить метр.
В экспедиции участвовали Пьер Мешен (1744-1804) и Жан-Батист-Жозеф Деламбр (1749-1822). Мешен, страстный охотник за кометами, сотрудничал с Лапласом при расчете орбит некоторых небесных тел, а Деламбр по просьбе Лапласа осуществлял астрономические наблюдения, необходимые для расчетов небесной механики. Два неутомимых астронома отправились в путь в 1792 году, когда в стране бурлил революционный хаос: Деламбр — к северу, до Дюнкерка, а Мешен — к югу, до Барселоны. Деламбр казался энергичным и воодушевленным, тогда как Мешен скорее отличался педантизмом и мнительностью, однако они преследовали одну цель — точно определить длину метра, то есть десять миллионных расстояния между Северным полюсом и экватором.
Измерить дугу меридиана было нелегким делом. Нельзя было напрямую рассчитать расстояние между Дюнкерком и Барселоной (этому мешали неровности рельефа), а ученым необходимо было точное значение вдоль воображаемой прямой линии, которая проходила бы над низменностями и пронзала бы горы и холмы. Для решения задачи они воспользовались методом триангуляции: благодаря тригонометрии можно измерить расстояние между двумя точками, взяв за ориентир церковные колокольни или башни замков, куда можно подняться. Деламбр и Мешен чертили воображаемые треугольники и понемногу покрывали расстояние, разделявшее Дюнкерк и Барселону. Они использовали повторительный круг Борда, который позволял сделать измерения значительно более точными. Этот инструмент позволял геодезистам многократно измерять один и тот же угол последовательно всеми частями разделенного круга, чтобы уменьшить ошибку углового измерения. И действительно, если вместо однократного измерения угла произвести измерение, например, десять раз, а затем сложить результаты и разделить сумму на десять, то можно значительно снизить возможность ошибки.
Вопреки планам Академии для измерений понадобилось не десять, а шесть лет. Объяснялось это сложной политической ситуацией: Франция вела войну с половиной Европы, в частности с Нидерландами и Испанией. Деламбр завершил свои измерения и триангуляцию 2 августа 1797 года в Родезе и ожидал там Мешена. Однако его коллега был тяжело ранен в Испании (впоследствии он потерял из-за этого способность управлять рукой) и на некоторое время вынужден был остаться в Барселоне. Когда Мешен, наконец, прибыл в Родез, то вручил Деламбру результат с погрешностями. Из-за военного конфликта он не смог выбрать в качестве ориентира барселонский замок Монжуик, расположенный в зоне боевых действий, и ориентировался на другую точку, посчитав, что это не скажется на точности измерений. Однако такое отклонение вызвало погрешность, равную трем секундам дуги. Эта ошибка отразилась на результате вычислений и, как следствие, на длине метра.
В 1798 году, после почти семи лет приключений, Деламбр и Мешен представили свои измерения в Институт Франции, который определил точную длину метра. Мешен умолчал об отклонениях в измерении, но муки совести не позволили ему оставить все как есть, и ученый решил провести свою часть измерений заново. При этой повторной попытке Мешен погибнет. Метр, определенный Деламбром и Мешеном, оказался короче современного на 0,2 миллиметра — эта погрешность не имеет никакого значения в повседневной жизни, но является важной для современных технологий.
В первой половине 1799 года Лаплас предложил организовать первый международный научный конгресс в истории, чтобы представить на нем новую систему мер и весов. От имени Директории Талейран пригласил все союзные и нейтральные державы. В конгрессе приняли участие девять стран, включая Нидерланды и Испанию. Они отправили в Париж нескольких своих ученых, которые должны были узнать о работе, проведенной во Франции, и сообщить об этом в своих странах. Французскую сторону представляли Лагранж, Лаплас и Лежандр, а также Деламбр и Мешен. Они с большой пышностью представили гостям эталоны метра и килограмма, отлитые из платины. Эти эталоны и сегодня хранятся в Парижской обсерватории — хотя метр больше не определяют как одну десятимиллионную четверти дуги меридиана. Сегодня метр — это путь, пройденный светом в вакууме в течение 1/299792458 секунды. «Завоевания приходят и уходят, — сказал Наполеон Бонапарт,— но это открытие останется навсегда».
МЕТОД ТРИАНГУЛЯЦИИ
Представим себе, что Деламбр и Мешен хотят измерить расстояние между городами А и В, но между этими точками высится постоянное препятствие, гора С, как показано на схеме.
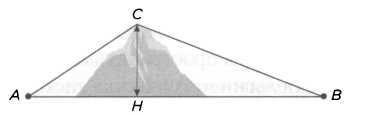
При помощи теодолита или, для большей точности, повторительного круга Борда они могут измерить углы, с которых можно наблюдать вершину горы в обоих городах, то есть угол А треугольника АСН и угол В треугольника ВСН. При помощи барометра, измеряющего давление по отношению к высоте, можно узнать высоту горы, или расстояние между Н и С. Применяя к этим данным правила тригонометрии, делаем вывод, что тангенс угла А равен высоте НС, разделенной на расстояние АН. Тангенс угла В равен высоте НС, разделенной на расстояние ВН. Выделив неизвестное из АН и ВН в обоих выражениях и сложив их, получаем:
AB = AH + HB = HC/tg(A) + HC/tg(B),
то есть расстояние между городами А и В.
Однако введение новых единиц измерения столкнулось с трудностями. Народ не понимал значения этих странных греческих и латинских префиксов — кило- и санти-. Пришлось подключать пропаганду. В сентябре 1801 года был принят закон, запрещающий использование других систем измерения, помимо метрической, но действовал он только на бумаге. Через несколько лет, в 1812 году, Франция вернулась к традиционным единицам. Один из поэтов высмеивал метрическую систему: «Неужели для того, чтобы выпить стакан вина, отрезать локоть материи или починить часы, действительно необходимо измерить дугу меридиана?» Однако хотя метрическая система не была признана в самой Франции, завоевания Наполеона помогли распространить ее за пределы страны. В Нидерландах и Бельгии метрическая система установилась в 1820 и 1830 годах соответственно, хотя сама Франция, эту систему запатентовавшая, в это время все измеряла по старинке. Метрическая система будет применена в ней лишь в 1840 году, когда Шарль Эмиль, сын Лапласа, станет президентом комиссии, которая предложит вернуться к метрической системе, как этого хотел его уже покойный отец. Время подтвердило правоту Лапласа. Германия ввела эту систему в 1868 году, а Соединенные Штаты Америки и Великобритания все еще сохраняли прежние единицы измерения.




