Несмотря на всю свою ученость, Зенон впутался в крупные неприятности. Около 435 года до н. э. он вступил в заговор против тирана Элеи, Неарха, и провозил оружие для его свержения. К несчастью для Зенона, Неарх узнал о заговоре, и Зенон был схвачен. Рассчитывая узнать, кто были его сообщники, Неарх подверг Зенона пыткам. Скоро Зенон стал умолять палачей прекратить пытки и пообещал назвать своих сотоварищей. Когда Неарх приблизился, Зенон настоял на том, чтобы тиран подошел совсем вплотную, потому что лучше было сохранить имена заговорщиков в секрете. Неарх наклонился к Зенону. Неожиданно тот вцепился зубами в ухо Неарха. Неарх закричал, но Зенон не отпускал. Палачи смогли заставить его разжать зубы, только зарезав его. Так погиб повелитель бесконечного.
Со временем другой древний грек превзошел Зенона в вопросе бесконечного. Это был Архимед, эксцентричный математик из Сиракуз. Он был единственным мыслителем своего времени, бросившим взгляд в бесконечность.
Сиракузы были богатейшим городом острова Сицилия, а Архимед был их самым знаменитым жителем. О его юности мало что известно, по-видимому, он родился около 287 года до н. э. на Самосе, родине Пифагора. Перебравшись в Сиракузы, Архимед решал многие инженерные проблемы для их правителя, тирана Гиерона. Однажды тиран попросил Архимеда определить, изготовлена ли его корона из чистого золота или из сплава золота с серебром. Эта задача была не по силам всем ученым того времени. Однажды, погрузившись в ванну, Архимед заметил, что вода переливается через край. Он неожиданно подумал о том, что сможет измерить плотность короны и тем самым определить чистоту золота, погрузив ее в сосуд с водой и измерив объем вытесненной жидкости. Взволнованный своим прозрением, Архимед выскочил из ванны и побежал по улице Сиракуз, восклицая: «Эврика! Эврика!» и забыв о том, что совершенно гол.
Таланты Архимеда были полезны и войскам Сиракуз. В III веке до н. э. греческая гегемония прекратила существование. Империя Александра Македонского распалась на враждующие государства, и на Западе играла мышцами новая сила: Рим. И Рим имел виды на Сиракузы. Как говорит легенда, Архимед вооружил войско Сиракуз удивительным оружием для защиты города: катапультами, метавшими камни, мощными кранами, которые захватывали римские корабли, поднимали вверх и опрокидывали в воду, и зеркалами, отражавшими солнечный свет и таким образом на расстоянии поджигавшими римские суда. Римские солдаты так боялись этих боевых машин, что, увидев над стеной веревку или кусок дерева, обращались в бегство, думая, что это Архимед нацеливает свое оружие.
Архимед увидел бесконечность благодаря полировке своих зеркал. Греки уже не одно столетие интересовались коническими сечениями. Если рассечь конус плоскостью, можно получить окружности, эллипсы, параболы и гиперболы, в зависимости от того, под каким углом к оси конуса проведена плоскость. Параболическое зеркало обладает одной особенностью: оно собирает в точку солнечные лучи (или лучи от любого удаленного источника света) и фокусирует всю переносимую ими энергию на очень малой площади. Зеркало, которое смогло бы поджечь корабль, должно было быть параболическим. Архимед изучал свойства параболы и именно при этом впервые соприкоснулся с бесконечностью.
Чтобы понять особенности параболы, Архимед должен был научиться измерять ее. Например, никто не знал, как определить площадь части плоскости, ограниченной параболой и пересекающей ее прямой. Площади треугольников и кругов вычислять было легко; слегка менее правильные кривые, вроде параболы, были за пределами возможностей математиков того времени. Однако Архимед нашел способ измерить площадь параболы, используя бесконечное приближение. Первым шагом было вписать в параболу треугольник. В два маленьких незанятых пространства Архимед вписывал по треугольнику. После этого оставалось четыре еще меньших зазора, которые в свою очередь заполнялись вписанными треугольниками, и так далее (рис. 12). Это похоже на Ахиллеса и черепаху: бесконечная серия шагов, каждый из которых делается все меньше и меньше. Площади маленьких треугольников быстро приближались к нолю.
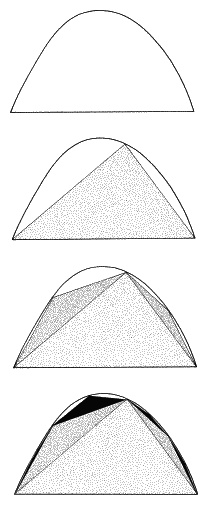
Рис. 12. Парабола Архимеда
После долгих и сложных вычислений Архимед сложил площади бесконечного числа треугольников и так нашел площадь параболы. Однако любой его современник отверг бы такое рассуждение: Архимед использовал такой инструмент, как бесконечность, который был категорически запрещен его коллегами-математиками. Чтобы их удовлетворить, Архимед предложил также доказательство, основанное на принятых тогда понятиях, использовавшее так называемую аксиому Архимеда, хотя сам Архимед приписывал заслугу ее открытия более ранним математикам. Как вы, возможно, помните, эта аксиома гласит, что любое число, снова и снова прибавляемое к самому себе, превзойдет любое другое число. Ноль, ясное дело, сюда не был включен.
Доказательство Архимеда с использованием треугольников было очень близко к идее предела и бесконечно малых, без их действительного открытия. В своих более поздних работах Архимед вычислил объемы тел вращения параболы и окружности вокруг прямой, что, как знает любой изучающий математику, есть одно из первых домашних заданий при изучении курса дифференциального и интегрального исчисления. Однако аксиома Архимеда отвергала ноль, который является мостом между областями конечных и бесконечных величин, мостом, абсолютно необходимым для дифференциального и интегрального исчисления и высшей математики.
Даже блестящий мыслитель Архимед иногда вместе со своими современниками пренебрегал нолем. Он верил в аристотелевскую вселенную, заключенную в гигантскую сферу. В шутку он решил вычислить, сколько песчинок заполнило бы (сферическую) Вселенную. В своем труде «Псаммит» («Исчисление песчинок») Архимед впервые подсчитал, сколько песчинок уляжется на семечке ромашки, сколько семечек ромашки уляжется на пальце… Перейдя от ширины пальца к стадию (стандартной греческой единице измерения расстояний), а затем к величине Вселенной, Архимед нашел, что Вселенную, заключенную во внешнюю сферу неподвижных звезд, заполнят 1051 песчинок. (1051 — это действительно очень, очень большое число. Если, например, взять 1051 молекул воды, то при условии, что каждый человек — мужчина, женщина и ребенок — будет выпивать по тонне воды в секунду, потребуется более 150 тысяч лет, чтобы такое количество воды было выпито.) Это число было настолько велико, что греческая система нумерации не могла с ним справиться. Архимеду пришлось изобрести новый способ записывать действительно огромные числа.
В греческой системе самым большим числом была мириада, и пересчитывая мириады, греки могли дойти до мириады мириад (100 000 000) и немного больше. Однако Архимед пошел дальше, «нажав кнопку перезагрузки». Он просто начал с мириады мириад, выбрав 100 000 000 в качестве единицы, и начал отсчет заново, назвав эти новые числа «числами второго порядка». (Архимед не считал 100 000 001 равным единице, а 100 000 000 — равным нолю, как поступил бы современный математик. Архимеду не приходило в голову, что начало с ноля было бы более осмысленным.) Числа второго порядка шли от мириады мириад до мириады мириад мириад мириад мириад мириад (1 000 000 000 000 000 000 000 000). Так продолжалось, пока Архимед не добрался до мириады в степени мириады, что он назвал числами первого периода. Это был очень громоздкий способ справиться с проблемой, однако так достигалось решение и даже давало гораздо большие возможности, чем Архимеду требовалось для его мысленного эксперимента.



