Как многие восточные религии, индуизм пропитался символизмом двойственности. (Конечно, эта идея периодически возникала в западном мире, где сразу же клеймилась как еретическая. Одним таким примером может служить манихейская ересь, которая рассматривала мир как находящийся под влиянием равных и противоположных сил — добра и зла.) Как инь и ян на Дальнем Востоке и зороастрийский дуализм на Ближнем Востоке, индуизм видел творение и уничтожение переплетенными между собой. Бог Шива был одновременно создателем и разрушителем мира и изображался с барабаном творения в одной руке и огнем разрушения в другой (рис. 13). Однако Шива одновременно олицетворял ничто. Один из аспектов этого божества, Нишкала Шива, буквально именовался «Шива без частей». Он был первозданной бездной, окончательным ничто — олицетворением безжизненности. Однако из бездны родилась Вселенная, как и бесконечность. В отличие от западной вселенной индуистский космос имел бесконечную протяженность; за пределами нашей Вселенной существовали бесчисленные другие вселенные.

Рис. 13. Танцующий Шива
В то же время, впрочем, космос никогда не лишался своей изначальной пустоты. Ничто было тем, из чего возник мир, и снова достичь ничто было окончательной целью человечества. В одной из легенд Смерть говорит ученику о душе: «В сердцах всех людей скрыт Атман, Дух, Самость. Он меньше мельчайшего атома и больше величайших пространств».
Этот Атман, присутствующий во всем, есть часть сущности Вселенной, и он бессмертен. Когда человек умирает, Атман освобождается из тела и скоро входит в другое существо; душа переселяется, и происходит реинкарнация. Целью индуиста является полное освобождение Атмана из цикла перерождений, прекращение блужданий от смерти к смерти. Путь к достижению окончательного освобождения — достижение безжизненности и пренебрежение иллюзией реальности. «Тело, обитель духа, находится под властью удовольствий и страданий, — говорит бог. — Если человек подчиняется своему телу, этот человек никогда не освободится». Однако стоит вам отделить себя от капризов плоти и погрузиться в безмолвие и пустоту своей души, и вы будете освобождены. Ваш Атман вылетит из сетей человеческих желаний и присоединится к коллективному сознанию — бесконечной душе, пронизывающей Вселенную, одновременно пребывающей всюду и нигде. Это — бесконечность и ничто.
Таким образом, Индия, общество, где активно исследовалась пустота и бесконечность, приняла ноль.
Реинкарнация ноля
В древние годы богов сущее родилось из не сущего.
Индийские математики сделали больше, чем просто приняли ноль. Они преобразовали его, изменив его роль: символа-заполнителя — на число. Эта реинкарнация и дала нолю его силу. Корни индийской математики скрыты временем. Индийский текст, написанный в год падения Рима — 476-й, — демонстрирует влияние греческой, египетской и вавилонской математики, которую принес Александр, вторгшийся в индийские земли. Как и у египтян, у индийцев были мерные веревки для разметки полей и закладки храмов. Индийцы имели изощренную систему астрономии; как и греки, они пытались рассчитать расстояние до Солнца. Для этого требуется тригонометрия; индийская версия была, возможно, создана на основании греческой. Примерно в V веке индийские математики изменили свой стиль нумерации. Они перешли от системы, сходной с греческой, к системе, похожей на вавилонскую. Важным отличием новой индийской системы чисел от вавилонской было то, что она была десятеричной, а не шестидесятеричной. Наши цифры возникли из символов, которыми пользовались индийцы; они по праву должны были бы называться индийскими, а не арабскими (рис. 14).
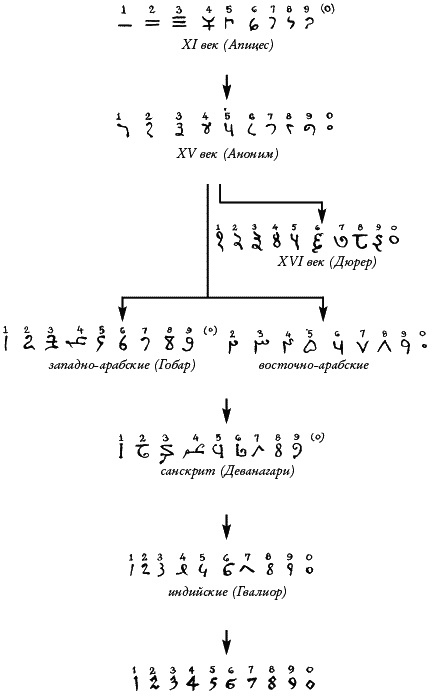
Рис. 14. Эволюция цифр:
Никто не знает, когда индийцы приняли вавилонскую позиционную систему счисления. Самое раннее упоминание об индийских цифрах можно найти у сирийского епископа, который писал в 662 году о том, что индийцы производят вычисления «посредством девяти знаков». Девяти, а не десяти. Очевидно, ноль не входил в их число. Однако утверждать с уверенностью трудно. Можно предположить, что индийские цифры были в ходу до того, как о них написал епископ. Имеются свидетельства, что к этому времени ноль стал появляться в каких-то вариантах, хоть епископ об этом и не слышал. Как бы то ни было, символ для ноля — символ-заместитель в десятеричной системе — к IX веку определенно был в употреблении. К тому времени индийские математики совершили огромный скачок. Они немногое позаимствовали из греческой геометрии; у них не было особого интереса к плоским фигурам, которые так обожали греки. Они не беспокоились о том, рациональна или нет диагональ квадрата; не изучали они и конические сечения, как это делал Архимед. Однако они узнали, как играть с числами.
Индийская система счисления позволяла использовать причудливые приемы при сложении, вычитании, умножении и делении без использования абака. Благодаря позиционной системе они могли складывать и вычитать большие числа примерно так же, как мы делаем сегодня.
При наличии тренировки человек мог, пользуясь индийскими цифрами, умножать быстрее, чем считающий на абаке. Соревнования между абакистами, считающими на абаке, и алгористами, как называли пользующихся индийскими цифрами, были средневековым эквивалентом матча между Каспаровым и «ДипБлю» (рис. 15). Как и «ДипБлю», алгористы в конце концов выигрывали. Хотя индийская система счисления была полезна в повседневных делах, позволяя складывать и умножать, ее истинное влияние было гораздо более глубоким.

Рис. 15. Алгорист против считающего на абаке
Числа наконец отделились от геометрии, они стали использоваться для большего, чем просто измерение объектов. В отличие от греков индийцы не видели квадратов в квадратных числах или площади треугольника, перемножая две величины. Вместо этого они видели взаимодействие чисел — чисел, лишенных их геометрического значения. Это было рождением того, что теперь мы знаем как алгебру. Хотя такой склад ума не позволил индийцам много внести в геометрию, он имел другое, неожиданное следствие. Он освободил индийцев от недостатков греческой системы мышления — и, в частности, отвержения ноля.
Поскольку числа лишились своего геометрического значения, математики могли больше не беспокоиться насчет того, что какие-то математические операции не имели геометрического смысла. Вы не можете скосить три акра травы с поля в два акра, но ничто не мешает вам вычесть три из двух. Сегодня мы знаем, что 2 — 3 = –1 (отрицательная величина). Впрочем, для древних это вовсе не было очевидно. Много раз, решая уравнения, они получали отрицательный результат и заключали, что их решение не имеет смысла. В конце концов, если вы мыслите в терминах геометрии, что такое отрицательная площадь? Для греков это была просто бессмыслица.





