Сегодня, когда возникают подобные вопросы, физики прибегают к открытому Нётер методу и получают однозначный ответ. Примените этот метод к релятивистским уравнениям движения Эйнштейна, и получите новую энергию, в которую войдет и энергия массы, mc². Применяя метод Нётер к квантовой физике, получите слагаемые, описывающие квантовую энергию.
Значит ли это, что «старая энергия» не сохранялась? Да, значит; если мы доработали уравнения, то, оказывается, не только частицы движутся иначе, чем предсказывалось ранее, но и вещи, которые, как мы считали, сохраняются, на самом деле не сохраняются. Классическая энергия больше не константа; мы должны включить в нее энергию, скрытую в массе, – и энергию квантовых полей. По традиции «энергией» системы называем сохраняемую величину. Так что, хотя сама энергия и не меняется со временем, меняется ее определение, поскольку мы продолжаем копать и открываем все более глубокие уравнения физики.
Подумайте вот о чем: правда ли те же самые физические уравнения, что работают в Нью-Йорке, действительны и в Беркли? Конечно. На самом деле такое наблюдение нетривиально; у него чрезвычайно важные следствия. Мы говорим, что уравнения не зависят от местоположения. Разными могут быть массы или электрические токи – но это все переменные параметры. Ключевой вопрос в том, различаются ли в разных географически местах уравнения, которые описывают физику поведения объектов и полей.
Уравнения, с которыми мы сегодня имеем дело в физике, – те, что входят в стандартную науку и экспериментально проверены, – работают всюду. Кое-кто считает это настолько поразительным, что тратит жизнь на поиск исключений из этого правила. Такие люди вглядываются в очень далекие объекты, как отдаленные галактики или квазары, и надеются увидеть, что там законы физики чуть-чуть отличаются от наших. До сих пор не удалось найти ничего подобного.
А теперь о замечательном следствии. Та же самая математика Нётер, что работает с уравнениями, не изменяющимися со временем, действительна также и для уравнений, которые не изменяются с местоположением. Воспользовавшись методом Нётер, мы можем найти комбинацию параметров (массы, координат, скорости, силы), которая и с переменой локации остается прежней. Применив эту процедуру к классической физике Ньютона, мы получим величину, равную произведению массы на скорость, – то есть классический импульс. Мы знаем, что импульс сохраняется, а теперь знаем также, почему сохраняется. Дело в том, что уравнения физики инвариантны относительно положения в пространстве.
Той же процедурой можно воспользоваться в теории относительности и квантовой физике, а также в их комбинации, известной как релятивистская квантовая механика. Комбинация, которая не меняется со временем, здесь выглядит немного иначе, но мы все равно называем ее импульсом. Она содержит релятивистские члены – а также электрическое и магнитное поля и квантовые эффекты, – но по традиции мы продолжаем называть ее импульсом.
Тесная связь между временем и энергией переносится и в квантовую физику с ее принципом неопределенности. Согласно квантовой физике, энергия и импульс части системы обычно неопределенные, хотя мы и можем их определить. Вероятно, нет возможности точно измерить энергию конкретного электрона или протона, но принцип не предусматривает аналогичной неопределенности для полной энергии системы. В большом наборе частиц энергия может перемещаться между различными частями системы, но полная ее энергия фиксирована; она сохраняется.
В квантовой физике поведение волновой функции во времени имеет слагаемое eiEt, где I = √−1, E – энергия, t – время. Когда Дирак решил свое уравнение для электрона, обнаружил, что в нем содержатся отрицательные энергии; именно это вынудило его предположить, что Вселенная представляет собой бесконечное море электронов с отрицательной энергией. Фейнман нашел этому другую интерпретацию. Он предположил, что отрицательной величиной оказывается не энергия E, а время t, тоже присутствующее в качестве сомножителя. Вместо отрицательной энергии у него появились электроны, движущиеся назад во времени, и Фейнман опознал в них позитроны.
В теории относительности физики видят пространство и время тесно переплетенными, а их комбинация носит название пространство-время. Инвариантность физики во времени ведет к сохранению энергии системы. Инвариантность в пространстве ведет к сохранению импульса. Если совместить то и другое, то инвариантность физики в пространстве-времени ведет к сохранению величины, известной как энергия-импульс. Ученые рассматривают энергию и импульс как два аспекта одного и того же. С этой точки зрения они скажут, что энергия – четвертый компонент четырехмерного вектора энергии-импульса. Если три компонента импульса обозначить как px, py и pz, то вектор энергии-импульса будет выглядеть как (px, py, pz, E). Разные физики расставляют эти четыре компонента в разном порядке. Некоторые считают энергию настолько важной, что ставят ее на первое место. Тогда они называют энергию нулевым, а не четвертым компонентом вектора: (E, px, py, pz).
Электрическое и магнитное поля тоже объединены в теории относительности, но более сложным способом. Вместо трехмерного вектора электрического поля (Ex, Ey, Ez) и трехмерного вектора магнитного поля, обычно записываемого (Bx, By, Bz), в теории относительности они становятся компонентами четырехмерного тензора F (от field – поле), который записывается так:
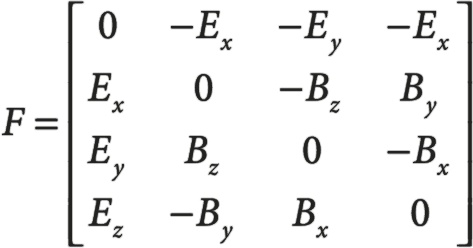
Матрица кажется сложной, и каждый компонент в ней повторяется дважды, но у нее есть преимущество: чтобы получить новый тензор F в другой системе отсчета, мы пользуемся теми же релятивистскими уравнениями, которые применяли при поиске пространственных координат и времени. Кроме того, вместо включения в наши уравнения отдельно электрического и магнитного полей просто включаем туда F. Уравнения при этом выглядят проще. Это позволило объединить электрическое и магнитное поля – то есть сделать их как бы частями одного более крупного объекта, тензора поля, а не двух отдельных сущностей.
Приложение 3
Доказательство иррациональности √2
Если предположить, что число √2 рационально, это будет означать, что это число можно записать в виде I/J, где I и J – целые числа. А теперь, если удастся свести это утверждение к противоречию, мы докажем, что наше первоначальное предположение ложно.
Если I и J четные, можем упростить дробь на общий делитель 2 и повторить это действие столько раз, сколько понадобится, чтобы хотя бы одно из этих чисел стало нечетным. Это значит, что если √2 = I/J, то можно записать также √2 = M/N, где по крайней мере одно из чисел M и N или оба нечетные.

