Современники среди прочего говорили о Фалесе, например, что он был необычайно рассеян. Фалес стал первым за долгое время ученым, о котором ходили слухи как о легкомысленном человеке. Согласно одной из легенд, гуляя ночью, он провалился в колодец, когда засмотрелся на звезды. Другая история повествует о том, что ученый погиб в возрасте восьмидесяти лет из-за того, что, увлеченный процессом, он совсем ничего не ел и не пил во время спортивного соревнования, на которое пришел посмотреть.
О некоторых смелых открытиях Фалеса сложили целые легенды. Так, он был первым, кто точно предсказал время солнечного затмения, которое произошло при битве между мидянами и лидийцами на реке Галис в восточной части современной территории Турции. Когда среди ясного дня наступила кромешная тьма, враждующие стороны посчитали это посланием бога и сразу же объявили перемирие. Для современных астрономов не представляет труда предсказать время затмения в будущем или определить, когда оно было в прошлом. Так, с предельной точностью можно сказать, что затмение, о котором шла речь выше, произошло 28 мая 584 г. до н. э. Так, битва при Галисе – самое раннее историческое событие, дата которого доподлинно известна!
Во время своего путешествия в Египет Фалес решил одну из сложнейших поставленных перед ним задач. Рассказывают, что фараон Амасис лично бросил ему вызов, предложив определить высоту пирамиды. До тех пор ни один из египетских ученых не смог этого сделать. Фалес не допустил поражения и использовал очень изобретательный способ. Ученый из Милета воткнул палку в землю под прямым углом и дождался момента, когда длина тени, отбрасываемой палкой, стала равна высоте палки. В этот же момент он измерил длину тени, отбрасываемой верхушкой пирамиды – это и была высота пирамиды. Ответ на загадку была найден!
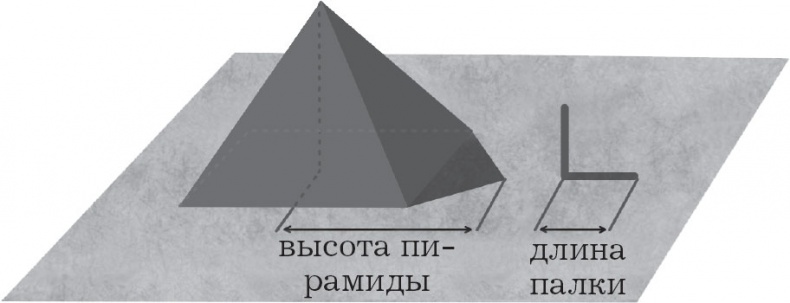
История зачастую иронична, и ее правдоподобность можно подвергнуть сомнению. Так, вопреки этой истории, высмеивающей несообразительность древнеегипетских ученых, в папирусе Ахмеса говорится о том, что в Древнем Египте прекрасно знали, как рассчитать высоту пирамиды, более чем за тысячу лет до Фалеса! И где же правда? На самом ли деле Фалес измерил высоту пирамиды? Стал ли он первым, кто применил метод определения ее высоты, используя данные о тени? Или же ему было достаточно измерить оливковое дерево во дворе своего дома в Милете? Последователей Фалеса подозревают в приукрашивании истории после его смерти. Стоит учитывать, что нам известно достаточно мало об этом.
Как бы там ни было, геометрия Фалеса вполне реальна, и, независимо, высоту пирамиды или оливкового дерева он измерил, метод использования тени не становится от этого менее гениальным. Этот способ – один из примеров того, что мы сегодня называем теоремой Фалеса. Ряд других математических достижений присваивают Фалесу: диаметр делит круг пополам (рис. 1), углы основания равнобедренного треугольника равны (рис. 2), вертикальные углы двух пересекающихся прямых равны (рис. 3), треугольник, вписанный в окружность, одна их сторон которого является диаметром окружности, – прямоугольный (рис. 4). Последнее утверждение также часто называют теоремой Фалеса.
Вернемся к нашему новому термину: что же такое теорема? Этимология этого слова состоит из греческих слов thÉa (созерцание) и horáô (смотреть, видеть). Таким образом, теорема – это что-то вроде наблюдения с математической точки зрения, то есть замеченное явление, за которым наблюдали и выводили из наблюдейний определенные закономерности математики. Теоремы могли передаваться как устно, так и письменно. Данный термин мог бы применяться и к бабушкиным рецептам и приметам, которые передавались из поколения в поколение и не подвергались сомнению. Одна ласточка весны не делает, лавровый лист лечит ревматизм, и один из углов треугольника, стороны которого относятся как 3–4–5, прямоугольный. Эти знания мы не подвергаем сомнению и можем использовать снова и снова.
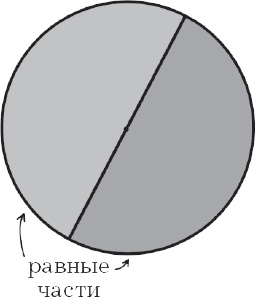
Рис. 1
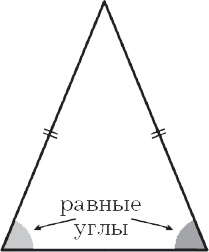
Рис. 2
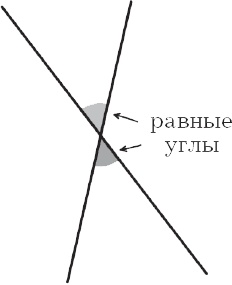
Рис. 3
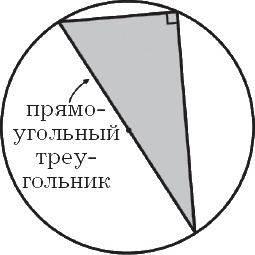
Рис. 4
Если рассматривать термин «теорема» так, как это описано выше, то жители Древней Месопотамии, Египта и Китая также имели свои теоремы. Однако начиная с Фалеса, древние греки начали использовать это слово в математическом значении: предполагалось, что теорема должна носить максимально обобщенный характер и подтверждаться доказательством.
Вернемся к одному из свойств, открытие которого приписывают Фалесу: диаметр делит круг пополам. Это утверждение могло бы показаться достаточно неоднозначным для ученого уровня Фалеса, ведь это очевидно. Как могло получиться так, что только в VI в. до н. э. люди пришли к такому очевидному выводу? Нет сомнений, что ученые Древнего Египта и Вавилона уже давно сделали это наблюдение.
Однако надо четко понимать, что имя ученого из Милета осталось в истории не только благодаря сделанному наблюдению, но прежде всего из-за сформулированного им доказательства. Фалес сформулировал эту теорему в общем виде – для любого круга! Чтобы сделать тот же вывод, ученые из древних Вавилона, Египта и Китая обращались к конкретным примерам. Нарисовав круг радиусом 3 и диаметр внутри него, они отмечали, что диаметр делит указанный круг пополам. Если одного примера не было достаточным для подтверждения данного факта, приводился второй, третий, четвертый примеры, если требовалось. Примеры приводились до того момента, пока не становилось очевидным, что это верно для любого подобного случая. Но никогда ранее не приводилось и не формулировалось обобщенное доказательство.
Фалес был в этом первооткрывателем. Он говорил о любом круге, независимо от его параметров. Он мог быть как гигантского размера, так и совсем крошечным, начерченный на горизонтальной, вертикальной или наклонной поверхности – совершенно не важно, какой конкретно круг. Всегда диаметр будет делить его на две равные половины.
Так, Фалес был первым, кто окончательно придал геометрическим фигурам статус абстрактных математических объектов. Этот этап в развитии по значению сопоставим с моментом, когда за две тысячи лет до этого в Месопотамии числа стали рассматриваться отдельно от исчисляемых объектов. Круг с этих пор перестает быть очертанием, сделанным на земле, глиняной табличке или папирусе, и перерастает в идею, абстрактную категорию, идеальную форму, реальные изображения которой отныне становятся не более чем условной иллюстрацией. С этих пор математические истины формулируются обобщенно, независимо от наличия конкретных примеров. Такие задачи древние греки теперь стали называть теоремами.







