Следуя по центральной дорожке сада, мы, словно по канату, идем по линии меридиана Парижа. Шаг влево, и мы оказываемся в восточном полушарии мира. Два шага вправо – и мы уже в Западном полушарии. Еще через пятьсот метров меридиан пересекает обсерваторию, тянется посередине 14-го округа Парижа, а затем выходит через парк Монсури. Далее он уходит за пределы города, частично проходит по территории Испании и устремляется через Африканский континент и Антарктический океан к Южному полюсу. С другой стороны он идет по улицам Монмартра, слегка соприкасается с Британскими островами и Норвегией, а затем устремляется к Северному полюсу.
Начертить линию меридиана было не так-то просто. Это требовало точных измерений колоссального масштаба. Как, например, узнать расстояние между двумя точками по разные стороны горы, не пересекая ее при этом? Для того чтобы ответить на этот вопрос, ученые в начале XVIII в. разметили траекторию меридиана, мысленно покрыв всю территорию Франции с севера на юг сеткой из треугольников.
В качестве точек триангуляции выбрали наиболее высокие географические объекты, такие как холмы, горы или башни, откуда можно было увидеть другие точки для измерения углов между ними. После проведения измерений на земле можно было в полной мере использовать тригонометрические методы, разработанные арабами, чтобы определить точное положение каждой точки триангуляции, а затем провести через них меридиан.
Одним из первых эту задачу будет решать Кассини. Род Кассини – это целая династия ученых, которых принято нумеровать, как царей! Джованни Доменико, именуемый Кассини I, только что эмигрировавший из Италии, был первым директором Парижской обсерватории с момента ее основания в 1671 г. После смерти Джованни Доменико в 1712 г. его преемником стал сын Жак, или Кассини II. Именно он в 1718 г. первым провел меридианы с помощью триангуляции. После этого Кассини III (Сезар-Франсуа, сын Кассини II) впервые полностью завершил триангуляцию всей территории Франции. Результатом его работы стала публикация в 1744 г. первой карты Франции, составленной полностью в соответствии с требуемой методикой. Сын Сезара Франсуа, Кассини IV, Жан-Доминик, продолжил эту работу и проводил триангуляцию одного региона за другим.
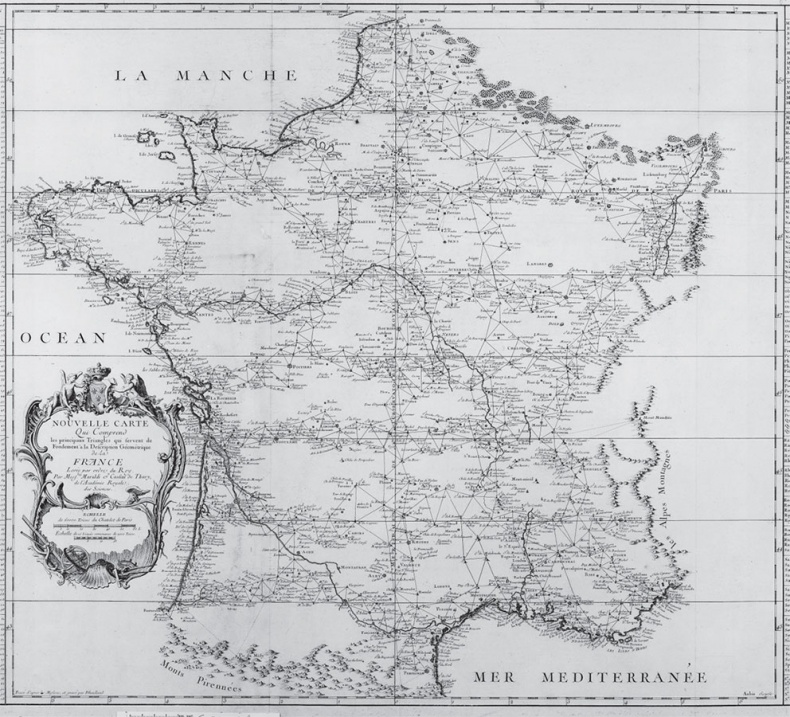
Карта Франции 1744: представлен меридиан, на котором находится Париж, и основные треугольники Кассини
Следуя по меридиану, мы практически идем по стопам арабских ученых, которые создали теоретическую основу для триангуляции. Разметка каждого треугольника на карте требует использования косинуса, синуса или тангенса. Все они есть наследие аль-Каши и первых багдадских ученых, занимавшихся тригонометрией. Все эти расчеты, сделанные вручную, потребовали бесчисленного количества часов, проведенных учеными, работавшими с тригонометрическими таблицами в обсерватории.
Расчеты с помощью триангуляции использовались вплоть до конца XX в., пока не появились спутники. Самая крупная сеть треугольников насчитывала до 80 000 точек. Особые знаки, которые отмечали эти точки, все еще можно встретить на всей территории Франции. В Париже вы можете увидеть две точки, через которые проходит ось меридиана: одна находится в южной части города в парке Монсури, другая – на севере, на Монмартре. В 1994 г. тридцать пять памятных знаков в честь астронома Франсуа Араго были установлены по линии меридиана, проходящей по территории Парижа. Один из них находится прямо в Лувре. В следующий раз, когда станете прогуливаться по улицам Парижа, будьте внимательнее, и, вполне возможно, заметите несколько из них.
Во время французской революции произошел переход на метрическую систему измерения и для универсальности длину 1 метра стали рассчитывать исходя из длины меридиана, а именно как одну десятимиллионную часть четверти длины меридиана. В 1796 г. в четырех концах Парижа установили шестнадцатиметровые камни для того, чтобы каждый мог увидеть эталон длины. По сей день два из них все еще можно увидеть: один – на улице Вожирар с видом на Люксембургский сад, другой – на Вандомской площади у входа в Министерство юстиции.
Парижский меридиан был общепризнанным ориентиром вплоть до международной конференции в Вашингтоне в 1884 г. С этого момента в качестве отправной точки признавали Гринвичский меридиан, проходящий через Королевскую обсерваторию в Лондоне. В свою очередь, англичане переняли у французов метрическую систему, которую используют по сей день.
С появлением компьютеров и спутников тригонометрические таблицы и триангуляция земли стали бесполезными. Но тригонометрия как таковая никуда не исчезла. Она находится в самом сердце процессоров. Треугольники скрыты, но они все еще там.
Достаточно взглянуть на автомобили, припаркованные на проспекте перед обсерваторией. Многие из них оснащены системой GPS. В каждую секунду их положение определяется четырьмя спутниками из космоса. Для определения положения в их вычислениях до сих пор используются тригонометрические свойства. Догадываются ли автомобилисты, что, пока голос подсказывает, что необходимо повернуть налево, процессор проводит вычисления синуса или косинуса?
А вы когда-нибудь замечали, как полицейские в детективных сериалах определяют местоположение телефона подозреваемого с помощью триангуляции? Суть данного метода сводится к тому, что положение сотового телефона определяется по расстоянию до трех ближайших антенн. Эта геометрическая задача решается без проблем благодаря тригонометрическим формулам – современные компьютеры молниеносно выполняют эти операции.
С помощью тригонометрии можно не только измерять существующие величины, но и конструировать виртуальную реальность. Достижения этой науки широко используются в создании 3D-анимационных фильмов и видеоигр. Под текстурами, обрабатываемыми графическими дизайнерами, скрываются 3D-формы, состоящие из геометрических сеток, странным образом напоминающие триангуляции Кассини. Именно благодаря деформации этих связей создаются объекты и фигуры. Моделирование даже самого простого 3D-изображения, как, например, чайник Юта, который был одним из первых объектов, созданных на компьютере в 1975 г., требует применения большого числа тригонометрических формул.

9
Навстречу неизвестному

Вернемся в Багдад. Особенный след в истории оставили работы одного из ученых, посещавших Байт аль-Хикму: его имя Мухаммад ибн аль-Хорезми.
Аль-Хорезми – персидский математик, родившийся в 780-х гг. Его семья жила в Хорезме, государстве, расположенном на территории современных Ирана, Узбекистана и Туркменистана. Нет однозначных данных, родился ли аль-Хорезми здесь или его родители эмигрировали в Багдад еще до его рождения, – доподлинно известно только то, что молодой ученый жил в Багдаде в начале IX в. Он был одним из первых ученых, работавших в Байт аль-Хикме и создавших ее репутацию как ведущего исследовательского центра своего времени.

