Использование символов стало настолько эффективным, что алгебра начала быстро развиваться автономно от геометрии. Исчезла необходимость изображать умножение в виде прямоугольников или применять доказательство в виде мозаики. Теперь все сводилось к определению x, y и z! Более того, стремительное развитие эффективности алгебраических конструкций с использованием букв в скором времени приведет к тому, что уже геометрия будет опираться на алгебраические доказательства.
Французский математик Рене Декарт будет основоположником эффективного способа решения геометрических задач алгебраическими методами с использованием системы осей координат.
Декартова система координат
Идея Декарта была одновременно элементарной и гениальной: начертить две размеченные линии, горизонтальную и вертикальную, с тем чтобы идентифицировать каждую геометрическую точку координатами по двум осям. Рассмотрим, например, следующую точку А:
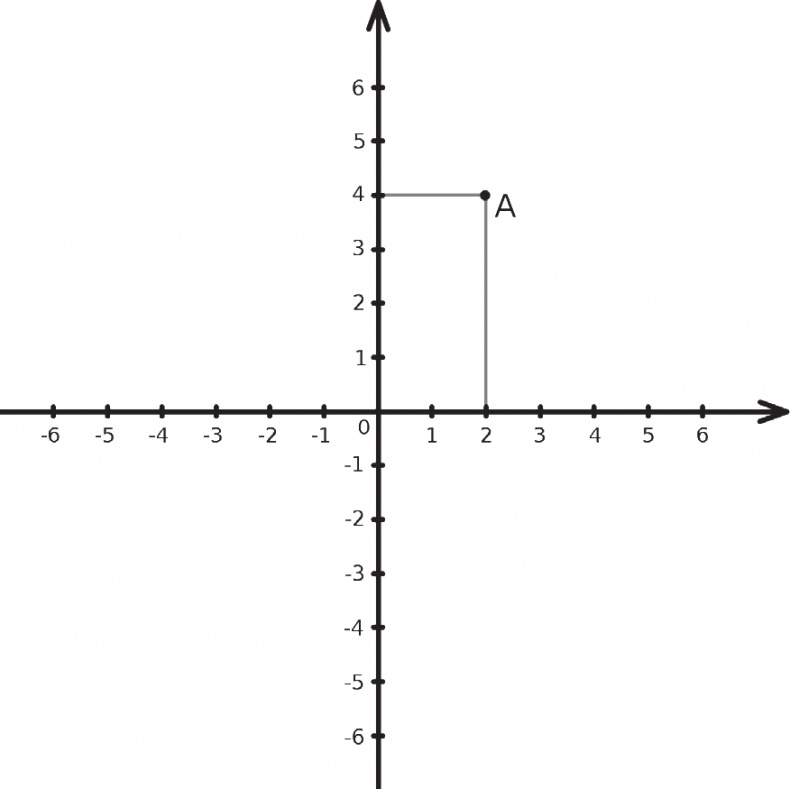
Точка находится на отметке 2 горизонтальной оси и 4 – вертикальной оси. Следовательно, ее координаты равны 2 и 4. С помощью этого метода становится возможным представлять каждую геометрическую точку двумя числами и, наоборот, находить точку для каждой пары чисел.
С момента своего возникновения геометрия и числа всегда имели тесные связи, но с появлением прямоугольной системы координат две эти дисциплины стали неразрывны. С того времени любая геометрическая задача могла решаться алгебраически, а алгебраическая задача – геометрически.
Рассмотрим, например, следующее уравнение первой степени: х = у + 2. Это уравнение с двумя неизвестными: необходимо найти х и у. Например, можно заметить, что х = 2 и у = 4 образуют решение, так как 2 + 2 = 4. Далее ясно, что числа 2 и 4 – это координаты точки А. Таким образом, можно представить это решение геометрически как точку.
На самом деле уравнение х + 2 = у имеет бесконечное количество решений. Например, пары чисел х = 0 и у = 2 или х = 1 и у = 3. Для любого значения х находится соответствующий у путем добавления 2. Теперь мы можем отметить в нашей системе координат все точки, соответствующие этим решениям. Таким образом, мы получим следующий график.
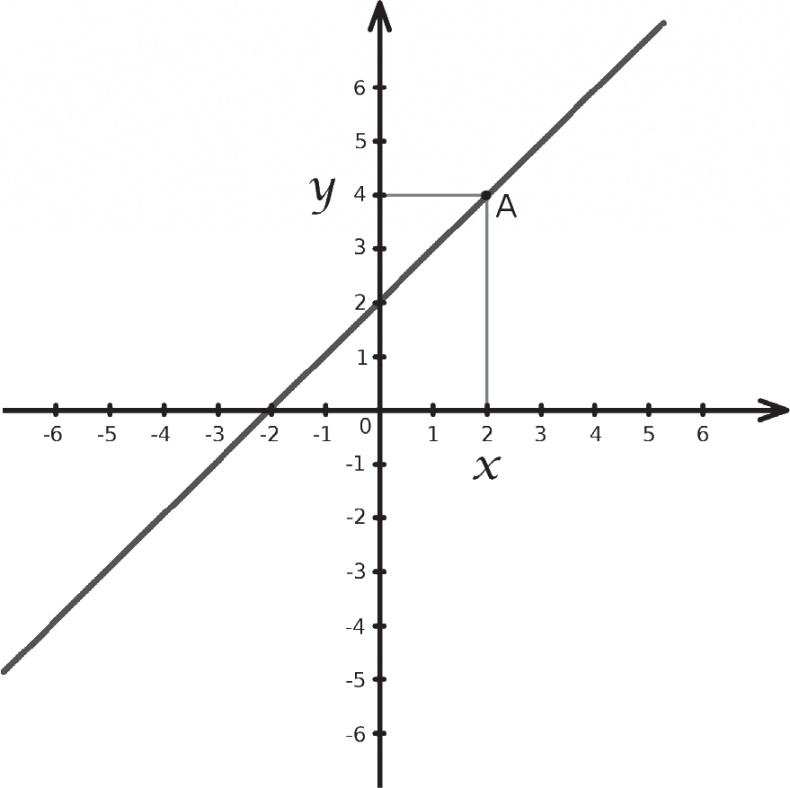
Прямая линия! Решения формируют идеально прямую линию. Нет ни одного из них, которое отклонялось бы от этого правила. В прямоугольной системе координат линия является геометрическим решением уравнения, а уравнение – алгебраическим представлением прямой линии. Два объекта слились воедино, и сегодня нередко можно услышать, как математики называют прямую линию х + 2 = y. Давая одни и те же имена разным вещам, алгебра и геометрия в действительности становятся единой дисциплиной.
Такая взаимозависимость привела к тому, что геометрические явления могут быть описаны алгебраическим языком и наоборот. Например, то, что называется «серединой» в геометрии, именуется «средним» в алгебре. Возьмем точку А с координатами 2 и 4 и соединим ее с точкой B с координатами 4 и 6. Для того, чтобы найти середину отрезка, соединяющего А и В, достаточно найти средние значения координат. Первые координаты А и В равны 2 и 4, соответственно, из чего можно сделать вывод о том, что первая средняя координата равна среднему значению этих двух чисел: (2 + 4) / 2 = 3. Аналогично можно найти среднее значение по вертикальной оси: (4 + (–6)) / 2 = –1. Таким образом, координаты середины отрезка равны 3 и –1, в чем можно убедиться, отметив эту точку на графике:
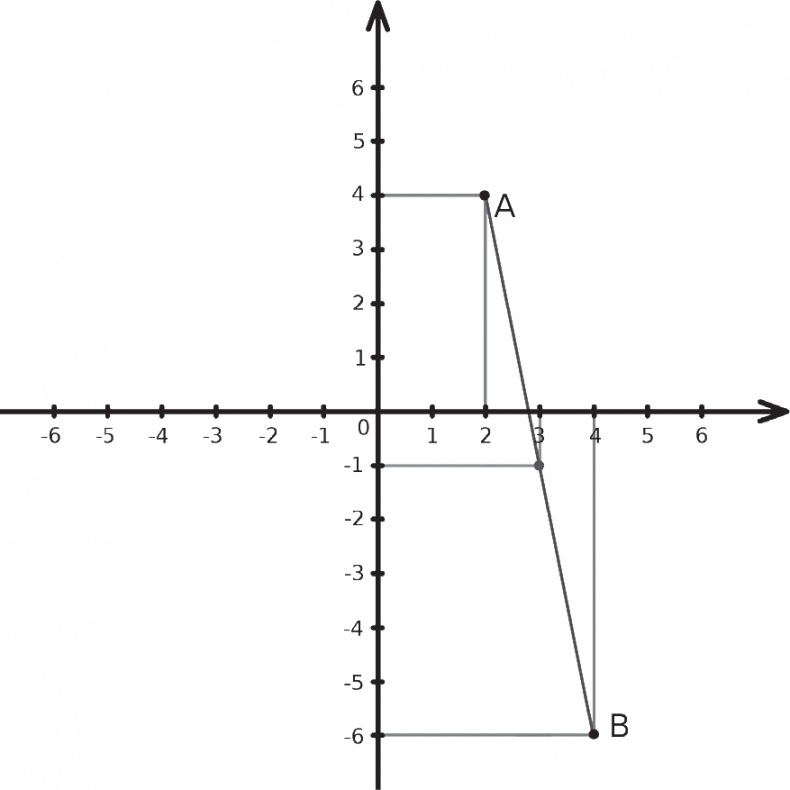
В словаре соответствий терминов из алгебры и геометрии окружность обозначает квадратное уравнение, точки пересечения двух окружностей – систему уравнений, а теорема Пифагора, тригонометрические конструкции и разделение на мозаичные части трансформируются в различные буквенные формулы.
Подводя итоги, можно сделать вывод, что в дальнейшем для решения геометрических задач не было необходимости изображать фигуры: алгебраические расчеты окончательно заняли свое место в математике, что значительно упростило и ускорило решение задач!
В последующие века использование прямоугольной системы координат способствовало достижению значительных успехов в развитии математики.
Одним из наиболее важных среди них было, несомненно, решение вопроса гипотезы, волновавшей умы математиков еще со времен Античности: определение квадратуры круга.
Можно ли с помощью линейки и циркуля начертить квадрат и круг, равные по площади? Вспомните, как еще более трех тысяч лет назад писец Ахмес уже пытался решить этот вопрос. После него разгадку безуспешно искали в Древнем Китае и Греции, но вопрос оставался на протяжении веков одной из величайших математических загадок, ответа на которую не было найдено.
В прямоугольной системе координат прямые линии, проведенные с помощью линейки, становятся линейными уравнениями, в то время как окружность, начерченная циркулем, может быть представлена в виде квадратного уравнения. С алгебраической точки зрения вопрос о квадратуре круга, таким образом, сводится к вопросу о том, можно ли найти такие уравнения первой и второй степени, решениями которых будет число π? Благодаря этой формулировке исследования возобновились, но вопрос все равно оставался сложным.
Только в 1882 г. немецкий математик Фердинанд фон Линдеман нашел окончательный ответ на этот вопрос. Нет, решением уравнений первой и второй степени не будет число π, и найти квадратуру круга невозможно. Таким образом, была решена проблема, которая до этого времени не поддавалась ни одному математику.
Прямоугольная система координат может легко быть расширена до пространственной геометрии. В трехмерной системе координат каждая точка будет иметь уже три координаты, и алгебраические методы могут быть применены к ним таким же образом.
Все становится несколько сложнее, когда мы переходим к четвертому измерению. С точки зрения геометрии невозможно представить себе фигуру в четырех измерениях, так как мы живем в трехмерном мире. В алгебре, однако, это не представляет сложности: значение координаты четвертого измерения – это все лишь четвертая строчка в координатной записи. И все алгебраические методы применимы в четырехмерном пространстве аналогичным образом. Например, если мы рассмотрим точки А и В, координаты которых равны 1, 2, 3 и 4 для первой точки и 5, 6, 7 и 8 для второй соответственно, можно без проблем найти среднее значение этих чисел: их координаты будут равны 3, 4, 5 и 6. Четырехмерная геометрия, в частности, использовалась в XX в. при формулировании теории относительности Альберта Эйнштейна, который станет использовать четвертую координату для моделирования времени.





