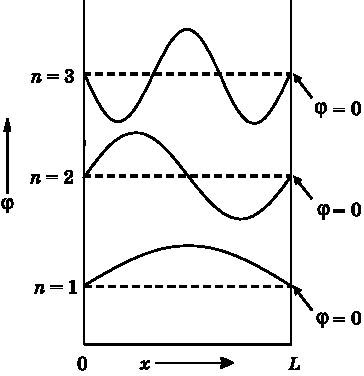
Рис. 8.4.Три примера волновых функций φ внутри ящика, которые являются непрерывными. Для ясности они сдвинуты друг относительно друга по вертикали. По вертикальной оси отложена амплитуда волновой функции. Штриховая линия показывает, где волновая функция равна нулю, что должно соблюдаться вне ящика. Волновые функции, имеющие нулевые значения на стенках, непрерывны на них
На рис. 8.4 приведены три примера волн, которые подходят на роль волновых функций для частицы в ящике. Нижняя из них обозначена n=1 и состоит из одной полуволны. Она начинается слева на амплитуде 0, проходит максимум и затем снова опускается до нуля на стенке в точке L. Следующая волна, расположенная выше и обозначенная n=2, состоит из одного полного колебания. Она тоже начинается у левой стенки на амплитуде 0, проходит положительный пик, возвращается к нулю, затем следует отрицательный пик и возвращение к нулю на стенке в точке L. Волна, обозначенная n=3, содержит полтора периода. Подходит любая волна, содержащая целое число полуволн, то есть 1, 2, 3, 4, 5 и так далее половин длины волны, и расположенная так, чтобы она начиналась на нуле слева и заканчивалась на нуле справа.
Величина n — это число полуволн конкретной волновой функции. При n=1 длина волны λ составляет 2L, поскольку длина ящика равна L, а n=1 соответствует половине длины волны. При n=2 длина волны составляет L, поскольку ровно одна длина волны помещается между стенками. При n=3 между стенками помещаются три полуволны, то есть 1,5λ=L. В этом случае λ=L/1,5, то есть λ=⅔L. Обратите внимание, что здесь обнаруживается общее правило: λ=2L/n, где n — целое число. Для n=1 получаем λ=2L, для n=2 — λ=2L/2, для n=3 — λ=⅔L и т. д.
Узлы — это точки, где волновая функция проходит через ноль
Узлы — это ещё одна важная особенность волновых функций. Узлы — это точки, где волновая функция пересекает нулевую линию, переходя от положительных значений к отрицательным или от отрицательных к положительным. Волновая функция n=1 не имеет узлов. У волновой функции n=2 один узел располагается ровно посередине ящика. Волновая функция n=3 имеет два узла. Узлы — это точки, где (помимо стенок) вероятность обнаружить частицу равна нулю. В классической системе, такой как на рис. 8.2, мяч движется взад-вперёд. Он может находиться в любом месте. Однако для частицы в квантовом ящике есть определённые места (узлы), где вероятность обнаружить её равна нулю. Сколько бы измерений идентично подготовленных систем ни выполнялось, мы никогда не обнаружим частицу в узле.
На рис. 8.4 изображены волны амплитуды вероятности. Как уже говорилось, вероятность обнаружить частицу в некоторой области пространства пропорциональна квадрату волновой функции (в действительности квадрату её абсолютной величины, но для наших целей это не важно). На рис. 8.5 представлены квадраты волновых функций, изображённых на рис. 8.4. Квадраты волновых функций всегда положительны, поскольку вероятность обнаружить частицу в некоторой области пространства не может быть отрицательной. Там, где амплитуда велика, частица может быть обнаружена с большей вероятностью. С увеличением n число узлов возрастает. В следующей главе и далее будет показано, что атомные и молекулярные волновые функции имеют узлы.
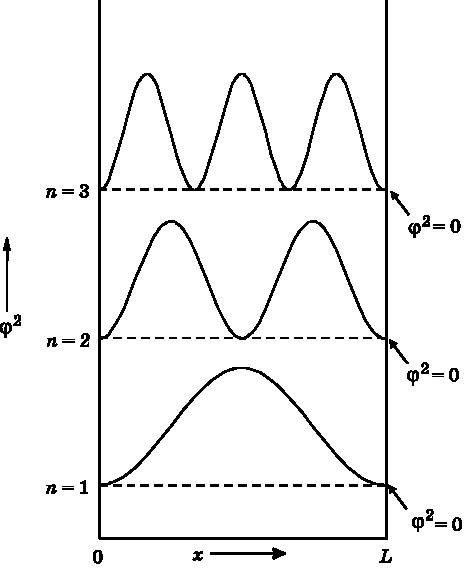
Рис. 8.5.
Квадраты первых трёх волновых функций
φ
2
для частицы в ящике. Для ясности они сдвинуты друг относительно друга по вертикали. По вертикальной оси отложен квадрат волновой функции амплитуды. Штриховая линия показывает, где волновая функция равна нулю. Квадраты волновых функций всегда положительны — они соответствуют вероятности. Волновые функции, изображённые на рис. 8.4, могут быть положительными или отрицательными
Часто спрашивают: как же частицы проходят через узлы? Например, при n=2 имеется узел, расположенный ровно посередине ящика. В классической системе, если мяч находится в левой части ящика и движется направо, но нам говорят, что он никогда не появится в центре ящика, то мы уверены, что мяч не достигнет правой стороны ящика. Однако такие рассуждения в классическом стиле неприменимы к абсолютно малым частицам, таким как электрон в ящике молекулярного размера. Он не обладает одновременно определёнными положением и импульсом, которые соответствовали бы наблюдаемой траектории. Квантовые частицы (в данном случае электрон) описываются как волны амплитуды вероятности. Волны имеют узлы. Они есть даже у классических волн. Квантовая частица «проходит через» узел, поскольку она является делокализованной волной амплитуды вероятности. Представление о траектории, двигаясь вдоль которой от точки A до точки B частица должна пройти все промежуточные точки между ними, просто неприменима к корректному волновому описанию электронов и других абсолютно малых частиц.
Значения энергии квантуются
Теперь мы определим возможные значения энергии, которой может обладать абсолютно малая частица в ящике. Классический мяч на ракетбольной площадке может иметь любую энергию, то есть набор её возможных значений непрерывен. Определить, какой энергией может обладать такая частица, как электрон в крошечном ящике, можно, опираясь на правило для возможных значений длины волны λ=2L/n амплитуды вероятности в этом ящике (см. рис. 8.4). Слово «крошечный» означает здесь, что ящик мал в абсолютном смысле, то есть длина волны сопоставима с его размерами. Нам также понадобятся несколько других физических соотношений, которые уже встречались нам ранее, а именно: соотношение для длины волны де Бройля p=h/λ, где p — импульс, а h — постоянная Планка; формула для импульса p=m∙V, где m — масса частицы, а V — её скорость; выражение для кинетической энергии частицы
E=½m∙V2.
Давайте объединим эти формулы.
Первым делом возведём в квадрат величину p:

