В действительности вопрос состоит в том, какова вероятность обнаружить электрон на некотором расстоянии от ядра, если сложить все возможные направления. Можно сформулировать этот вопрос иначе: какова вероятность обнаружить электрон в тонком сферическом слое радиусом r? Поскольку с увеличением r объём этого тонкого сферического слоя возрастает, то на некоторых расстояниях это нивелирует тот факт, что волновая функция убывает. Чтобы понять роль этого тонкого сферического слоя, рассмотрим ряд пустых резиновых мячей с одинаковой толщиной оболочки. Мяч маленького радиуса (r) будет содержать меньше резины, чем мяч большого радиуса. Если же вы просто пойдёте по одной прямой линии от центра мяча и, добравшись до его оболочки, поинтересуетесь толщиной резины, то она не будет зависеть от радиуса мяча. Ясно, однако, что в оболочке большого мяча содержится больше резины, чем в оболочке маленького.
Площадь поверхности сферы составляет 4π∙r2, где r — радиус сферы. Умножив эту величину на толщину оболочки, вы получите объём резины в мяче. Теперь ясно, что большой мяч содержит намного больше резины в своей оболочке, чем маленький. Если удвоить радиус, количество резины увеличится в 4 раза. Другой важный факт: когда r стремится к нулю, количество резины в мяче тоже стремится к нулю, поскольку к нулю стремится площадь поверхности 4π∙r2. Спрашивать, находится ли электрон на расстояние r от ядра, — это всё равно что спрашивать, сколько резины содержится в оболочке мяча радиусом r. Тут необходимо учитывать увеличение площади поверхности при увеличении радиуса.
Функция радиального распределения
Функция радиального распределения — это как раз то, что нужно для учёта трёхмерной природы атома. Чтобы по мере увеличения r учесть все направления поиска электрона, необходимо добавить множитель 4π∙r2. Функция радиального распределения задаёт вероятность обнаружить электрон на расстоянии r от ядра для всех направлений. В главе 5 говорилось, что, согласно интерпретации волновой функции Бора, вероятность обнаружить частицу в некоторой области пространства пропорциональна квадрату абсолютного значения волновой функции. Сейчас мы хотим найти вероятность обнаружения электрона в тонком сферическом слое радиусом r. Это и будет функция радиального распределения, задаваемая формулой 4π∙r2∙|Ψ|2. Вертикальные линии, как и прежде, обозначают абсолютную величину. Для функций, с которыми мы имеем дело, потребуется лишь возвести в квадрат волновую функцию.
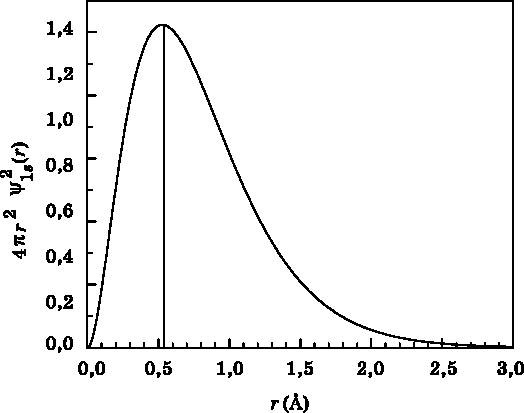
Рис. 10.4. График функции радиального распределения для 1s-орбитали в зависимости от расстояния r до протона. Функция радиального распределения — это вероятность обнаружить электрон в тонком сферическом слое на расстоянии r от протона. Функция радиального распределения учитывает тот факт, что электрон может быть найден в любом направлении от протона. Расстояние r измеряется в ангстремах (1 Å = 10−10 м)
На рис. 10.4 показана функция радиального распределения для 1s-состояния атома водорода.
Расстояние, на котором достигается максимальная вероятность, — это не центр атома, поскольку объём сферического слоя стремится к нулю, когда r обращается в нуль. Вертикальная линия показывает положение максимума распределения вероятности, который находится на отметке r = 0,529 Å. Это значение представляет особый интерес. В старой боровской квантовой теории атома водорода электрон в 1s-состоянии движется по круговой орбите радиусом 0,529 Å. Это расстояние называется радиусом Бора и обозначается a0. Корректное квантовомеханическое описание атома водорода гласит, что электрон — это волна амплитуды вероятности с расстоянием максимальной вероятности, равным радиусу Бора a0. Это не случайное совпадение. Радиус Бора в действительности является фундаментальной постоянной. Он определяется формулой
a0=ε0∙h2/π∙μ∙e2,
где все параметры те же, что и в выражении для постоянной Ридберга через фундаментальные постоянные. На самом деле энергетические уровни атома водорода можно выразить через радиус Бора следующим образом:
En=−e2/8π∙ε0∙a0∙n2.
На рис. 10.5 и 10.6 представлены графики волновых функций (вверху) и функций радиального распределения (внизу) для орбиталей 2s и 3s. Волновая функция для 2s-орбитали имеет узел, то есть место, где она обращается в нуль. Об узлах мы говорили в связи с волновой функцией частицы в ящике (см. рис. 8.4). Вблизи узла вероятность обнаружить частицу, в данном случае электрон, равна нулю. Волновая функция состояния 2s начинается с положительного значения, пересекает нулевое значение в узле, расположенном на расстоянии, равном удвоенному радиусу Бора (2а0), а затем становится отрицательной. Далее волновая функция спадает до нуля. На расстоянии 8 Å значение волновой функции уже очень мало́.
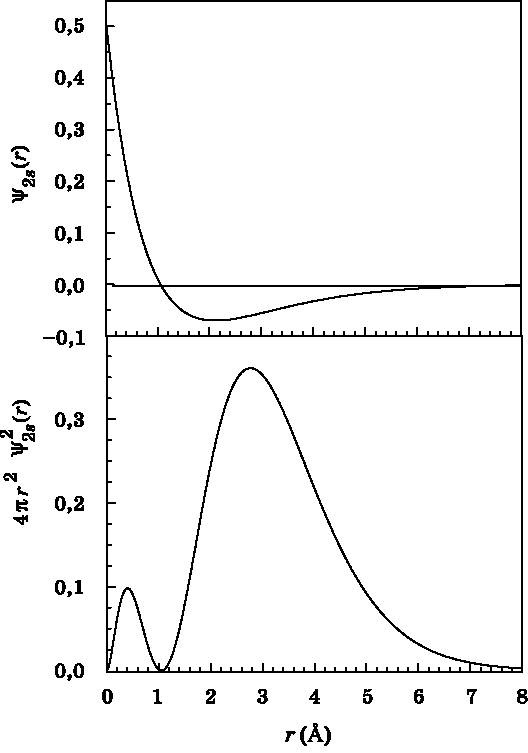
Рис. 10.5. Волновая функция (вверху) и функция радиального распределения (внизу) для 2s-орбитали атома водорода в зависимости от расстояния r до протона. Волновая функция начинается с положительного значения, проходит через узел чуть дальше точки 1 Å (2a0) и затем спадает до нуля. Функция радиального распределения демонстрирует максимум вероятности обнаружения электрона на отметке 2,8 Å, причём наиболее вероятно найти его в интервале от 2 до 4 Å (см. рис. 10.2). Расстояние r измеряется в ангстремах (1 Å = 10−10 м)
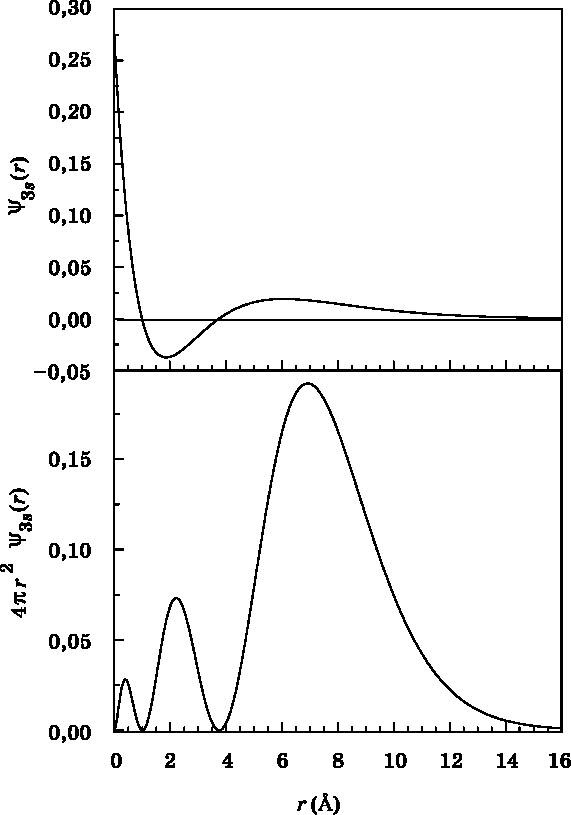
Рис. 10.6. Волновая функция (вверху) и функция радиального распределения (внизу) для 3s-орбитали атома водорода в зависимости от расстояния r до протона. Волновая функция начинается с положительного значения, проходит через узел, становясь отрицательной, проходит через второй узел, вновь становясь положительной, и затем спадает до нуля. Функция радиального распределения показывает, что вероятность обнаружения электрона достигает максимума на отметке 7 Å, причём наиболее вероятно найти его в интервале от 5 до 11 Å (см. рис. 10.2). Расстояние r измеряется в ангстремах (1 Å = 10−10 м)

