Почему углекислый газ поглощает именно в этой области?
Мы видим, что углекислый газ захватывает инфракрасное излучение вблизи пика земного черноте́льного излучения и что увеличение концентрации CO2 пагубным образом сказывается на температуре Земли. Но почему CO2 поглощает инфракрасное излучение именно вблизи частоты 667 см−1? В главах с 8-й по 11-ю мы обсуждали энергетические уровни частицы в ящике, атома водорода и всех остальных атомов. В главах с 12-й по 14-ю мы обсуждали молекулярные орбитали и связанные с ними энергетические уровни. Весь этот разговор вращался вокруг энергетических уровней для электронов. На основе представления о молекулярных орбиталях объяснялась природа химических связей, которые удерживают вместе атомы в молекулах. Однако мы не говорили о движениях атомов, которые соединены химическими связями в молекулы.
На рис. 12.1 изображена кривая потенциальной энергии для молекулы водорода H2. Эта кривая показывает, что энергия меняется в зависимости от расстояния между двумя ядрами атомов водорода. Длина химической связи — это расстояние, на котором энергия достигает минимума. Однако эта связь не является жёсткой. Если думать о ней в терминах классической механики, то связь — это пружина с двумя грузами — атомами водорода, присоединёнными к её концам. Пружина может растягиваться и сжиматься. В классической системе, если растянуть пружину и отпустить её, грузы начинают колебаться, вызывая попеременное растяжение и сжатие пружины. В случае классического осциллятора грузы будут колебаться вперёд-назад по хорошо определённой траектории. Опираясь на квантовую теорию, мы сразу должны заподозрить, что у квантовых колебаний не может быть такой хорошо определённой траектории, иначе это означало бы, что мы точно знаем и положение, и импульс частиц (атомов). Для абсолютно малых систем, таких как атомы, связанные в молекулу, это нарушало бы принцип неопределённости Гейзенберга.
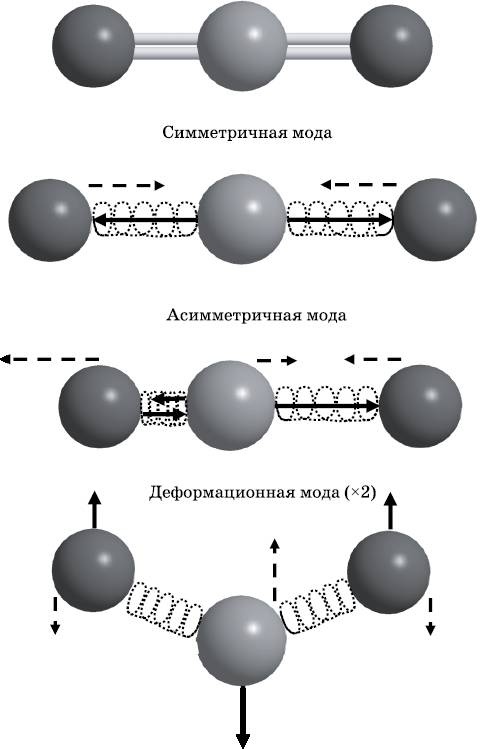
Рис. 17.2.
Вверху: шаростержневая модель молекулы углекислого газа CO
2
. Внизу: три различные колебательные моды молекулы. Имеется две деформационные моды: одна из них изображена, а ещё одна такая же связана с движением атомов в направлении, перпендикулярном плоскости страницы
На рис. 17.2 изображена шаростержневая модель углекислого газа CO2, а также показаны возможные её колебательные движения. Молекула CO2 — линейная с двумя атомами кислорода, которые связаны двойными связями с центральным атомом углерода. Молекула CO2 может совершать четыре различных колебательных движения, называемых колебательными модами. Связи могут растягиваться и сжиматься, а также деформироваться. Связи изображены пружинками. Чтобы понять природу этих колебательных мод, мы будем описывать соответствующие им движения так, как если бы они совершались классическими шариками на пружинах.
Колебательные моды углекислого газа
В симметричной моде центральный атом углерода не двигается. Как показано на схеме сплошными стрелками, два атома кислорода удаляются от углерода, растягивая пружины. Затем эти два атома возвращаются обратно к центральному атому углерода, сжимая пружины, что показано штриховыми стрелками. В классической системе из шаров на пружинах это движение повторяется, так что координаты атомов периодически меняются. Частота этих колебаний определяется массой грузов и упругостью пружин. В асимметричной моде два атома кислорода сначала сдвигаются вправо. Левый атом кислорода сжимает пружину, а правый растягивает её. Колебания не вызывают сдвига молекулы в целом. Поскольку оба атома кислорода движутся вправо, атом углерода смещается влево, сохраняя положение молекулы неизменным. Поскольку углерод движется влево, когда атомы кислорода смещаются вправо, в среднем положение всех атомов, называемое центром масс, не меняется. Эти движения обозначены сплошными стрелками. Затем направление движения каждого атома меняется на противоположное, как показано пунктирными стрелками.
Симметричные и асимметричные растяжения оставляют все три атома на одной прямой. В деформационной моде два атома кислорода сдвигаются вверх, а атомы углерода — вниз. При этом центр масс остаётся на месте. Затем атом углерода начинает двигаться вверх, а два атома кислорода — вниз. Кроме деформационной моды, изображённой на рис. 17.2, существует ещё одна. В нарисованной моде движения атомов происходят в плоскости страницы. Вторая деформационная мода точно такая же, за исключением того, что атомы движутся поперёк плоскости страницы.
Квантовые колебания обладают дискретными уровнями энергии
В классическом осцилляторе, сделанном из шаров, соединённых пружинами, энергия системы может меняться непрерывным образом. Рассмотрим симметричную моду. Три шара, связанные двумя идеальными пружинами, лежат на столе; трение и сопротивление воздуха отсутствуют. Если, взявшись за два внешних шара, в одинаковой мере растянуть две пружины и отпустить, то шары будут совершать симметричные упругие колебания. Поскольку пружины идеальные, трение о стол отсутствует и нет сопротивления воздуха (в реальной жизни такого, конечно, не бывает), колебания будут продолжаться вечно. Период и частота этих колебаний не зависят от того, насколько сильно были растянуты пружины. Период определяется упругостью пружин и массами шаров. Если растянуть пружины лишь чуть-чуть, то шары будут двигаться медленно. Их средняя кинетическая энергия будет мала. Если растянуть пружины сильно, шары станут двигаться быстро, а их средняя кинетическая энергия окажется велика. Энергия колебательной системы из шаров на пружинах меняется непрерывным образом. Она зависит только от того, насколько сильно мы растянем пружины.
Молекулы в действительности не являются шарами на пружинах. Это квантовомеханические системы, состоящие из атомов, соединённых химическими связями. Вместо непрерывного спектра энергий квантовые системы обладают дискретными колебательными энергетическими уровнями. Квантование их энергии происходит точно так же, как в задаче о частице в ящике, обсуждавшейся в главе 8. Герхард Херцберг (1904–1999) получил Нобелевскую премию по химии в 1971 году
«за вклад в понимание электронной структуры и строения молекул, особенно свободных радикалов».
Работа Херцберга по определению строения молекул основывалась во многом на его объяснении колебательных спектров молекул.
Энергия классического мяча для ракетбола меняется непрерывным образом, но энергия квантового мяча (частицы в ящике) привязана к энергетическим уровням (см. рис. 8.6). На рис. 17.3 изображена потенциальная кривая для вибрационной моды молекулы, подобная представленной на рис. 12.1, но теперь на ней также отмечены первые несколько колебательных энергетических уровней. И вновь, как и в случае частицы в ящике, низший энергетический уровень n=0 не соответствует нулевой энергии.

