Это все «очень вероятные» двери!
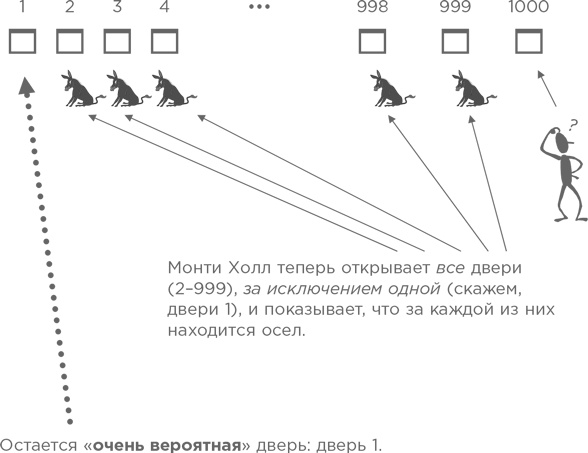
Теперь мы готовы ответить на вопрос. Какой выбор будет наилучшим?
• Дверь 1000 («очень маловероятная» дверь) или
• Дверь 1 («очень вероятная» дверь)?
Ответ теперь очевиден. Мы должны выбрать «очень вероятную» дверь, т. е. «передумать» — это лучшая стратегия для участника шоу. В экстремальной ситуации намного легче увидеть лучшую стратегию, чем при анализе ситуации с тремя дверями, как в исходных условиях задачи. Принцип одинаков в любой ситуации.
Эта задача вызвала немало споров в научных кругах и даже попала на страницы газеты The New York Times и других популярных изданий. Джон Тирни написал в The New York Times (Sunday, July 21, 1991), что «возможно это только иллюзия, однако похоже спору, в котором участвовали все от математиков до читателей журнала Parade и любителей телеигры Let's Make a Deal, положен конец. Спор начался, когда Мэрилин вос Савант опубликовала головоломку в журнале Parade. Как известно читателям ее колонки „Спросите Мэрилин“, имя г-жи вос Савант включено в списки Галереи славы Книги рекордов Гиннесса за обладание „наивысшего IQ“. Но этот факт производит на публику не такое впечатление, как то, что она сумела ответить на вопрос читателя». Мэрилин дала правильный ответ, и, хотя многие математики продолжают спорить, мы решили эту задачу!
Глава 6
Решение более простой аналогичной задачи
Некоторые задачи на первый взгляд кажутся чрезвычайно сложными. Смутить могут, например, очень большие числа. А иногда в замешательство приводит излишнее количество данных, некоторые из которых совершенно не нужны для решения. Даже формулировка задачи способна поставить в тупик. Что бы там ни было, отличный подход — упростить задачу, однако так, чтобы она осталась эквивалентной исходному варианту. Попробуйте уменьшить числа, изменить рисунок или как-то иначе упростить задачу. Решая упрощенную версию, вы получаете представление о том, как справиться с исходной задачей.
Купив первый раз новый компьютер, вы ведь не брались за освоение сразу всех функций и возможностей, а, скорее всего, начинали с чего-то более знакомого и постепенно добавляли новое, пока не выясняли, на что способно приобретение. Наверняка вы брались сначала за более простые функции.
Допустим, вам нужно решить следующую задачу:
Дано 19 последовательных целых чисел, сумма которых равна 95. Какое число стоит на десятом месте в этом ряду?
Одни, скорее всего, попробуют применить алгебраический подход и представят 19 целых чисел, как x, (x + 1), (x + 2), (x + 3), …, (x + 17), (x + 18) и так далее. Так они дойдут до 95, а потом найдут решение для x. Другие заметят, что число в десятой позиции является средним, обозначат его как x и представят остальные числа следующим образом: (x + 9), (x + 8), (x + 7), …, (x − 7), (x − 8), (x − 9). Теперь можно объединять парные члены по мере их добавления, т. е. преобразовывать (x − 9) и (x + 9) в 2x, (x − 8) и (x + 8) тоже в 2x и т. д., получая каждый раз 2x. Такая версия намного проще для решения, поскольку мы получаем уравнение вида 9(2x) + x = 95, или 19x = 95 откуда x = 5.
Вместе с тем есть еще более интересный подход. Допустим, мы рассматриваем более короткий ряд чисел, например 3 + 4 + 5 + 6 + 7. Их сумма (25) при делении на 5 дает среднее, а именно 5, которое оказывается средним числом ряда. Для ряда в нашей задаче средним число является 10-й член, а поскольку целые числа последовательны, этот член является также средним арифметическим, или средним числового ряда из 19 членов. Таким образом, чтобы найти среднее, нужно просто взять сумму (95) и разделить ее на количество членов ряда (19). Ответ — 5. Эта упрощенная версия задачи позволяет представить исходное задание в значительно более простой форме и, таким образом, облегчить решение.
Зачастую можно не ограничиваться простым уменьшением сложности исходной задачи, а применить также и другие наши стратегии. Например, найдите десятичное значение числа 1/500 000 000 000.
Воспользоваться калькулятором здесь не удастся, поскольку дисплеи большинства из них не воспроизводят 12-значные числа. Применим две другие стратегии: организуем данные и найдем закономерность. Решим ряд более простых версий нашей задачи, представим результаты в табличной форме, а потом посмотрим, нет ли в них какой-либо закономерности.
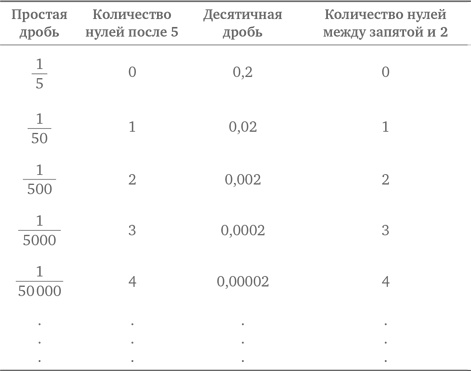
Здесь определенно просматривается закономерность. Количество нулей в знаменателе равно количеству нулей между запятой и 2. Поскольку в знаменателе 11 нулей после 5, между запятой и 2 должно быть тоже 11 нулей:
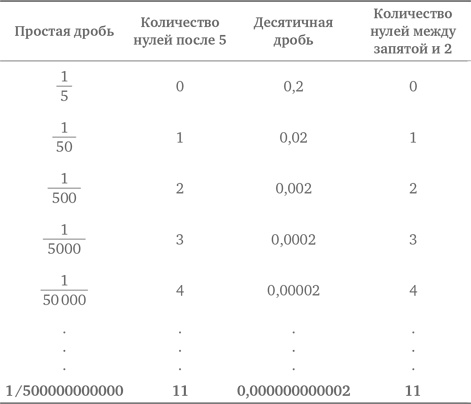
Обратите внимание, насколько упрощенная версия(и) исходной задачи вместе с двумя другими стратегиями облегчают решение. Имейте в виду, что использование нескольких стратегий для решения задачи не редкость.
Задача 6.1
Баскетбольная команда принимает участие в конкурсе на лучшее исполнение штрафных бросков. Первый игрок успешно выполняет x штрафных бросков, второй — y, а третий — количество бросков, равное среднему арифметическому количества бросков первых двух игроков. Каждый последующий игрок успешно выполняет такое количество бросков, которое равно среднему арифметическому бросков всех предыдущих игроков. Сколько успешных штрафных бросков сделает 12-й игрок?
Обычный подход
Некоторые пытаются решить такую задачу через определение среднеарифметического значения для каждого из 12 игроков по очереди. На это нужно много времени и сил. К тому же очень легко сделать ошибку при вычислениях. У задачи наверняка должно существовать более рациональное решение.
Образцовое решение
Мы начнем с анализа более простой аналогичной задачи. Заменим x и y простыми числами и посмотрим, что происходит. Допустим, первый игрок сделал 8 штрафных бросков (x), а второй — 12 (y). Тогда счет третьего игрока будет равен их среднему арифметическому, т. е.
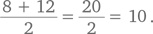Четвертый игрок наберет среднее арифметическое бросков первых трех игроков, т. е.
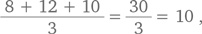а пятый — среднее арифметическое бросков первых четырех игроков, т. е.
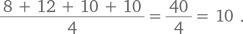Ну вот! Счет любого игрока после первых двух всегда равен среднему арифметическому успешных бросков первых двух игроков. Правильным ответом на эту задачу будет среднее арифметическое успешных бросков первых двух игроков, а именно
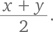Упрощенная аналогичная задача позволила нам определить метод, который нужно использовать для быстрого решения исходной задачи.
