Однако я рекомендую научиться использовать арифметику вычетов. В дальнейшем это очень пригодится. Это как с таблицей умножения: можно вызубрить её в том виде, в каком она приводится на тетрадных обложках. А можно понять правила умножения, и тогда без проблем перемножать любые числа.
Теперь давай научимся расшифровывать тексты, записанные шифрами многоалфавитной замены. Например, у тебя оказалось зашифрованное послание и ты знаешь, что оно зашифровано именно таким шифром. Как подступиться к расшифровке? Вот простейший метод:
1. Определить длину ключа, то есть длину цикла, в котором меняются алфавиты. Это делается при помощи одного очень хитроумного способа, о котором ты узнаешь чуть позже.
2. Как только длина ключа установлена, у нас появляется столько шифрограмм (зашифрованных шифром одноалфавитной замены), из скольких символов состоит ключ. А взламывать такие шифрограммы ты уже умеешь, то есть твоя задача сводится к тому, что мы изучили на прошлой неделе. Да, в этот раз расшифровка намного более трудоёмкая, поскольку придется несколько раз подсчитывать частоты и выдвигать гипотезы, а это непросто. Кроме того, надо суметь не запутаться и сопоставить расшифровки друг с другом. Но при должном умении и старании все получится.
Чтобы узнать длину ключа, используются два метода. Один из них очень трудоёмкий и требует множества вычислений (в наше время их можно поручить компьютеру, а раньше ими обычно занималась целая комната специально обученных сотрудников со счётами или счётными машинками). Но этот метод гарантированно определяет длину ключа. Ты можешь прочитать о нем в специальной литературе или справочниках — он называется «метод индекса совпадений ».

А вот второй метод — именно что хитроумный, но не всегда работает. Его мы и изучим. Он называется «метод Фридриха Касиски»
[1]. Идея заключается в том, что в обычном языке, на котором говорят люди, очень часто повторяются некоторые группы символов. Это коротенькие словечки или даже буквосочетания вроде многочисленных «ОРО» и «ОЛО» в русском языке. Грамотный шифровальщик избегает использования коротких словечек (об этом мы уже рассуждали на прошлой неделе), но вот с частыми буквосочетаниями это сделать сложно. Так что надо искать в шифрограмме такие повторяющиеся буквосочетания.
Итак, в шифрограмме мы ищем повторяющиеся группы символов. Лучше всего, чтобы длина этих групп была не менее трёх символов: если будет меньше, то велик шанс пойти по ложному следу. Это происходит из-за того, что разные двухбуквенные сочетания из шифруемого текста были зашифрованы при помощи разных символов в ключе, а в результате получились одинаковые буквосочетания в шифрограмме. Если группа символов длиннее, то такого практически не происходит.
Расстояния между последовательными появлениями одинаковых групп в шифрограмме будут кратны длине ключа. Так что мы подсчитаем расстояния между всеми этими группами, а длина ключа будет равна наибольшему общему делителю всех расстояний.
Иногда это не срабатывает, так как из-за использования большого числа алфавитов разные группы символов исходного текста могут случайно получиться одинаковой группой в шифрограмме. Такое возможно, если текст очень большой. Тогда криптоаналитик должен внимательно изучить разные возможности и отсеять то, что не подходит. Мы не будем практиковаться в этом занятии, но я должен сказать о том, что такая возможность есть.
После того как длина ключа определена, вся шифрограмма выписывается в колонку. Ее ширина равна количеству символов в ключе. Затем надо сделать частотный анализ (который мы изучили на первой неделе) для каждого столбика этой колонки.
Давай потренируемся во всем этом на практике. Представь себе, что ты видишь такое послание:
ТИЪРУЫМТУНРШАТПЮАКЧЧЙАЙТГЗУШМНОЧЖАЧЗСЦСЮЙЗЗЫХШЮХАФЭБ ДЦПЯХИСЫУХЮЭАППЖХКТУИЩЩЖЗЭШУЗЭЫШНТБАЩЪБЗХЮЦПЗЭШПЙДБЕРЫ БАЧ БТЪЮТПФАЫЗБМБЪФЯЫХЮТГЩФТСИАДШРБОГИБНАККВПУЭСУВООЦТБАИЫХФ ФЕЙФДДРДТПЧФГБЯЧЭАРОФЭЪЙТЛШПЭМНОХОРЫУУНЪНОГЫТРЦЛЕПФВТЛИЩТ ЙЗСТРШЮЛМГШТСИЦТ ЗДБШЫОЪБЖСЫУВОБАЧЮЯОЦШТВНАВПУФЪОЦАЕЙЗБУЛРДТЩРГГПКОЮБТЮЭА ЙКТОРОФЭУПТЕУЧАБЗЩЯЯПТЩРГГПЛ ТНФПТГЗЩБОНЖАПФПЫУЦТШАЙВЧЖЪОХИУЮБХПТУНЫТЛЦЫЖАРЭЕЖШФДОЦ ОШЖЗАБЕНЩЙФЮШАХЮТВУПЦПМПГЗЛЕПФВТФЧУЗХФАЙЕОЕЭЗВЩЖЗЫБЗНЗНА ЧЮА ЪЙТЙЗЯБЕЫЫУУВОАБЗБШНЫОЮБТОПОЭБАРЦЖХЧЕЫЗЛЕПЪОДРЦАБВЗЗЫХШЮХ БХЧСАББВГОБОЗАЕБУОУВЩЮЯЯЪЭБАХФХИУПЭКПШНГЫТЕНЪБС
Если сделать здесь частотный анализ, то получится вот такая таблица:
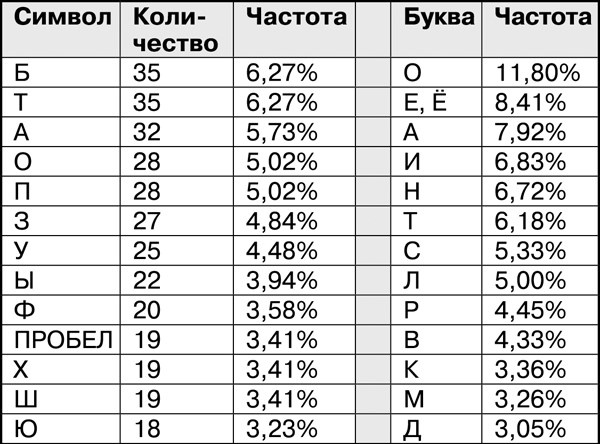
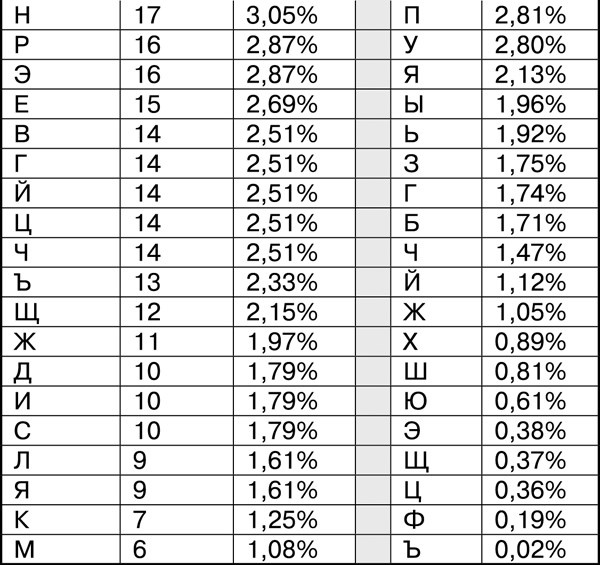
Для удобства в двух крайних правых столбцах этой таблицы я привел частоты букв в русском языке. Уже беглый взгляд на эту таблицу подсказывает, что тут есть проблема. Частоты совершенно не совпадают, хотя длина шифрограммы значительная (558 символов).
Что делают настоящие криптоаналитики для анализа подобной ситуации? Они строят графики. Вот два графика (они называются «гистограммами»):

Гистограмма частот символов в шифрограмме
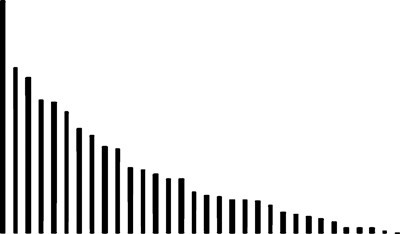
Гистограмма частот букв русского языка
Ты можешь представить себе, что эти графики — набор вертикальных штырьков, на которые нанизаны блины, как в детской пирамидке или головоломке «ханойская башня». Количество блинов на штырьке соответствует количеству целых процентов, а последний блин по толщине соответствует долям процента. Если расположить эти башни по убыванию количества блинов, то как раз получатся такие гистограммы. По горизонтали отложены буквы по убыванию частот их в языке, а по вертикали — относительные частоты в процентах.
Видишь, на этих графиках обозначены подсчитанные частоты символов. На левом графике отложены частоты символов из шифрограммы, а на правом — частоты букв русского языка. Вид графиков различается: для шифрограммы он более пологий. Это уже указывает на то, что нарушено распределение частот, а значит, для шифрования был избран не одноалфавитный шифр, а что-то другое. Кстати, в качестве тренировки рекомендую построить такую гистограмму для символов из шифровки первой недели: ты увидишь, что она очень похожа на гистограмму частот для букв русского языка.







