Том приводит пример уэльского круга Майл-тай-Уча (рис. 25) и считает, что здесь строители предприняли что-то совершенно отличное от того, что ранее пытались сделать в других местах. По словам Тома, они начали с круга диаметром 14 МЯ и, следовательно: 3 1/7×14 = 44 МЯ в окружности. Это, заключает он, не отвечало их целям, так как они хотели сделать периметр кратным 2 1/2 МЯ. Тогда, предположил Том, они придумали метод строительства уплощенных секций круга, которые с минимальными отклонениями сократили его до окружности в 42 1/2. Для этого требовалось минимум два радиуса, каждый из которых должен был быть интегральным. В добавление законченный круг для соответствия остальным должен был иметь ось симметрии. Но и это еще не все. По мнению Тома, чтобы установить азимут точки восхода звезды Денеб (альфа Лебедя), требовалось соблюсти еще одно внешнее условие. В рассматриваемое время Денеб восходил в азимуте 17,3°. По предположению Тома, строители хотели отразить это в своей конструкции так, чтобы пересечение осей указывало как на восходящую звезду, так и на истинный север. Но вместо азимута в 17,3° строители получили 18°. Он утверждает, что этот угол дополняет 72°, одну пятую от 360°. Хотя поздние греческие геометры показали, как строить угол в 72°, мегалитические строители могли добиться этого только методом проб и ошибок. Том показал, как это можно сделать, вычерчивая дуги на земле.
Второй изученный Томом круг находится в Истер-Делфоре в Шотландии. Там внешний каменный круг частично погребен под мусором. Том считал, что изначальная форма монумента представляла собой полую пирамиду из камней. Он говорил, что это заложено в размерах внутреннего круга, диаметр которого равен 8 МЯ, и что у этого круга много общего с кругом в Майл-тай-Уча, но он состоит из четырех частей, а не из пяти. Используя геометрические конструкции, Том опять же утверждал, что внешний диаметр круга составляет 22 МЯ, а меньшего по размеру внутреннего круга – 6 1/2 МЯ. Он был убежден, что открыл геометрию объекта, предполагая a priori модули его строительства (рис. 26).

Рис. 25. Майл-тай-Уча. В В находятся два внешних упавших камня (по А. Тому)
Третий круг из этой группы находится в Керри-Поул в Уэльсе. Том начал свои рассуждения с заявления о том, что это «маловпечатляющий» объект. Реконструкция его геометрии основывалась на кругах с диаметром 32 и 16 МЯ. Его геометрические доводы опять же весьма убедительны и представлены в безукоризненном стиле. Том нашел все радиусы интегральными: 16,8 и 30 МЯ, а периметр лишь на 0,12 отличался от значения, кратного его большей части в 2 1/ МЯ.
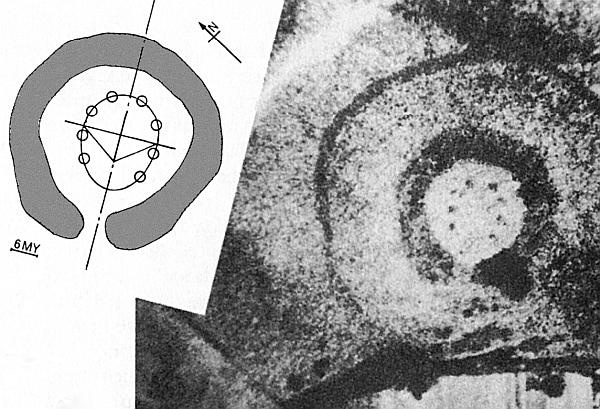
Рис. 26. Истер-Делфор (по А. Тому)
Идеи Тома относительно геометрической реконструкции мегалитических кругов получили свое полное развитие в его объяснениях главного круга Эйвбери и его меньших, внутренних кругов. Эйвбери, естественно, является гораздо более крупным объектом и поэтому более сложным в техническом исполнении при использовании примитивных «цепных» методов. Теодолитный ход собственного исследования Тома составлял 900 м (3000 футов) в длину и в трех точках контролировался астрономическим определением азимута. Он полагал, что его собственная финальная ошибка составляла всего 18 см (0,6 фута).
Том считал, что без знания точной длины мегалитического ярда в случае с Эйвбери вряд ли удалось бы реконструировать его плановую конструкцию. Вместе с тем он доказал, что Великий круг имел несколько дуг с различными радиусами, размеры двух из которых составляли 750 МЯ.
Приходилось признать, что, поскольку раскопана только половина круга, остальная его часть остается менее определенной. В одной секции только один камень остался стоять вертикально. Том начертил свою конструкцию на восковой бумаге, приняв модуль мегалитического ярда в 2,720 фута. С его точки зрения, если принять значение в 2,730 фута, то большой круг окажется больше почти на 1,5 м (5 футов) и выйдет за пределы оставшихся камней. Таким образом, Том получил «потрясающее доказательство» того, что МЯ был реальной величиной и именно той единицей, которую использовали строители Эйвбери для разметки размеров своего круга.
Метод Тома для интерпретации сложных мегалитических кругов, позволивший ему лично разобраться в конструкции Эйвбери, является типичным метрическим методом для всех изученных им кругов. По его словам, он мог доказать, что его определение МЯ и его предпочтительных интегралов, использованных при строительстве кругов, имеет прочную статистическую основу. Однако что касается астрономических интерпретаций, которые следуют из его реконструкций и предположений, то эту проблему было гораздо сложнее решить с помощью строгих статистических методов. Несмотря на это, он приводит список из 250 линий, обнаруженных во время его топографических исследований («Мегалиты Британии»). Большинство из перечисленных звездных ориентировок такие же, как у звезд Локьера: сначала идут звезды первой величины или наиболее яркие звезды, такие как Капелла, Ригель, Кастор и Поллукс, Денеб, Антарес, Беллатрикс, Спика, Альтаир, Арктур и Процион. Все эти звезды приведены к азимутам для дат между –2000 и –1500, поскольку по археологическим свидетельствам это был именно тот период, когда были построены круги и связанные с ними сооружения. Этот список содержит множество предполагаемых ориентировок на Солнце. Его радикальное отличие от работы Локьера заключается в том, что последняя содержит многочисленные ориентировки на Луну.
Том перечисляет астрономические азимуты, предоставленные:
1) куском камня;
2) двумя или более камнями, расположенными близко друг к другу;
3) кругом и близко расположенным внешним камнем;
4) двумя кругами.
Но для Солнца и Луны существуют следующие минимальные требования:
1) удлиненная линия ориентировки;
2) два достаточно далеких друг от друга камня;
3) круг, имеющий отдаленный ориентир примерно в сотне футов от него, или
4) естественный ориентир в виде некоего простого индикатора.
Том считал, что эти звезды использовались для определения времени. Их можно наблюдать во время восхода, при кульминации на меридиане (линия наблюдателя север – юг) или при заходе. Имеются прямые письменные доказательства тому, что греки со времен Гесиода и далее использовали звезды именно таким образом (возможно, этот метод был позаимствован из более ранней традиции верхнего палеолита). Например, в пьесе Еврипида один из персонажей спрашивает: «Какая звезда проходит сейчас?» На что получает ответ: «Плеяды показались на востоке, а Орел парит на вершине небосклона». Во времена ранних египетских династий, начиная с с. –2150, аналогичным образом использовались плеяды звезд или созвездия (деканальные). Эти деканальные звездные часы изображены на крышках многих гробов, и эту традицию ремесленники продолжали еще долгое время после эпохи, когда списки восходов деканальных созвездий имели какое-либо научное значение для определения времени. Позже, в период Рамсеса, были разработаны более сложные звездные часы, но их использование, похоже, было забыто еще задолго до того, как на египетской астрономии сказалось влияние идей вавилонян и греков. Карты звездного неба, публиковавшиеся в Европе вплоть до XVII века, содержат ту же информацию, что и современные планисферы.




