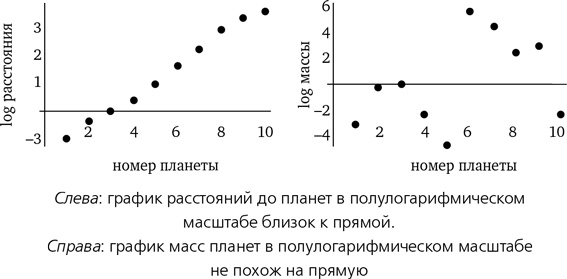
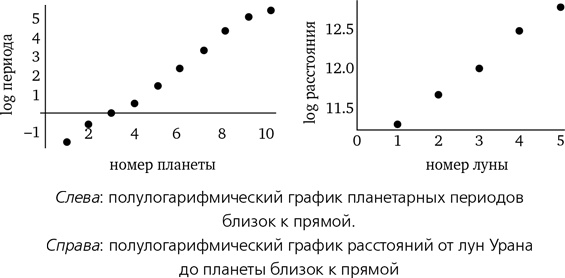
А орбитальный период? Вновь чистая прямая (смотри следующий график слева). Однако это неудивительно, поскольку третий закон Кеплера соотносит период с расстоянием таким образом, что степенная зависимость сохраняется. Попробуем расширить поле исследования и проверим пять основных лун Урана; получим график справа. Вновь степенная зависимость.
* * *
Совпадение или что-то более глубокое? Мнения астрономов разделились. В лучшем случае наблюдается тенденция к степенной зависимости в расстояниях. При этом зависимость не универсальна.
Здесь вполне возможно какое-то рациональное объяснение. Наиболее вероятное начинается с идеи о том, что в динамике случайной системы планет принципиально важную роль играют резонансы — случаи, когда орбитальные периоды двух планет дают в отношении простую дробь. К примеру, один из периодов может составлять 3/5 от другого, это резонанс 5:3
[26]. Не обращая внимания на остальные тела, эти две планеты будут то и дело — через правильные интервалы — выстраиваться вдоль радиальной прямой, связывающей их со звездой, потому что пять оборотов одной планеты вокруг звезды в точности соответствуют трем оборотам другой планеты. За долгий период времени возникающие при этом небольшие возмущения орбит будут накапливаться, так что планеты будут склонны менять свои орбиты. В то же время для периодов, отношение которых не дает простой дроби, возмущения, как правило, компенсируются, поскольку в таких системах нет преимущественного направления, вдоль которого могла бы действовать связывающая две планеты сила тяготения.
И это не просто неопределенное предположение: оно подтверждается детальными расчетами и обширной математической теорией. В первом приближении орбита небесного тела представляет собой эллипс. На следующем уровне аппроксимации наблюдается прецессия эллипса: его большая ось медленно поворачивается в пространстве. Еще более точная аппроксимация показывает, что доминирующие члены в centerх движения небесных тел возникают от вековых (секулярных) резонансов — более общего типа резонансных отношений между периодами, с которыми прецессируют орбиты нескольких тел.
Как именно движутся тела, находящиеся в резонансе друг с другом, зависит от отношения периодов, а также от их координат и скоростей, но часто результатом бывает очищение подобных орбит. Компьютерное моделирование показывает, что случайным образом распределенные вокруг звезды планеты склонны занимать позиции, отношения между которыми примерно похожи на закон Тициуса — Боде, а промежуточные позиции вычищаются резонансами. Но все это достаточно неопределенно и расплывчато.
В Солнечной системе есть несколько «миниатюрных» подсистем, роль которых играют планеты-гиганты со своими лунами. Орбитальные периоды трех крупнейших спутников Юпитера — Ио, Европы и Ганимеда — относятся друг к другу как 1:2:4, то есть каждый последующий из них вдвое больше предыдущего (см. главу 7). Четвертый спутник этой группы — Каллисто — имеет период немного меньший, чем удвоенный период Ганимеда. Согласно третьему закону Кеплера, орбитальные радиусы тел связаны аналогичным отношением, только множитель 2 следует заменить той же двойкой в степени 2/3, что дает нам коэффициент 1,58. То есть орбитальный радиус каждого спутника должен быть примерно в 1,58 раза больше орбитального радиуса предыдущего спутника. Это тот случай, когда резонанс не расчищает, а стабилизирует орбиты, и отношение расстояний здесь 1,58 вместо 2 по закону Тициуса — Боде. Тем не менее расстояния тоже подчиняются степенному закону. Сказанное можно отнести также к лунам Сатурна и Урана, как указал Стенли Дермотт в 1960-е
[27]. Такое распределение спутников называют законом Дермотта.
Расстояния, связанные степенным законом, представляют собой более общую закономерность, в которую входит и хорошая аппроксимация закона Тициуса — Боде. В 1994 году Беранжер Дюбрюль и Франсуа Гране, применив два общих принципа, вывели степенной закон распределения расстояний для типичных коллапсирующих солнечных туманностей. Оба принципа основаны на симметрии. Облако обладает осевой симметрией; кроме того, распределение вещества в нем примерно одинаково на всех масштабах измерения — это масштабная симметрия. Осевая симметрия динамически обоснована, потому что асимметричное облако непременно либо разорвется, либо станет со временем более симметричным. Масштабная симметрия типична для важных процессов, влияющих, по мнению ученых, на формирование планет, таких как турбулентные потоки внутри солнечной туманности.
Сегодня мы в состоянии выглянуть за пределы нашей Солнечной системы. А там такое начинается! Орбиты известных экзопланет — планет у других звезд — расположены на самых разных расстояниях, в большинстве своем совершенно непохожих на те, что мы наблюдаем у себя в Солнечной системе. С другой стороны, известные экзопланеты всего лишь непредставительная выборка из множества всех существующих планет; часто мы видим у звезды только одну планету, хотя там, вероятно, присутствуют и другие. К тому же методы, имеющиеся у нас на данный момент, обнаруживают прежде всего крупные планеты, обращающиеся близко к своему центральному телу.
До тех пор пока мы не получим полные планы планетных систем множества звезд, мы не сможем по-настоящему понять, что представляют собой экзопланетные системы. Однако в 2013 году Тимоти Бовэ и Чарльз Лайнуивер, рассмотрев 69 экзопланетных систем, в которых достоверно имеется не менее четырех планет, выяснили, что 66 из них подчиняются степенным законам. Исследователи попытались также при помощи полученных степенных зависимостей осторожно предсказать «недостающие» планеты, то есть повторить в экзосистемах историю с Церерой. Из 97 планет, предсказанных таким образом, пока удалось обнаружить лишь пять. Даже с учетом сложностей, связанных с обнаружением небольших планет, результат не оправдал надежд.
Все это достаточно неопределенно, поэтому внимание ученых переместилось на другие принципы, которые могли бы объяснить, как устроены планетные системы. Эти принципы опираются на тонкие особенности нелинейной динамики и не являются совсем уж эмпирическими. Однако числовой характер этих закономерностей менее очевиден. В частности, Майкл Делниц математически показал, что поле тяготения Юпитера, судя по всему, организовало все остальные планеты в единую взаимосвязанную систему, соединенную природными «трубками». Эти трубки, которые можно распознать только при помощи их математических характеристик, представляют собой естественные низкоэнергетические пути между разными мирами. Эту идею и связанные с ней вопросы мы обсудим в главе 10, куда они впишутся более естественно.




