* * *
В 1612 году Галилей, определив орбитальные периоды звезд Медичи, предположил, что достаточно точные таблицы их движения обеспечат моряков небесными часами и помогут разрешить навигационную проблему определения долготы. В то время мореходы умели определять широту места, наблюдая Солнце (хотя до точных инструментов вроде секстана было еще далеко), но долготу могли оценивать только по счислению пути, то есть методом очень приблизительного подсчета. Основной практической проблемой было проведение наблюдений с палубы качающегося на волнах судна, и Галилей работал над двумя устройствами для стабилизации телескопа. Метод Галилея использовался на суше, но не на море. А проблему долготы, как известно, решил Джон Харрисон при помощи серии точнейших хронометров, за что и получил в 1773 году призовые деньги.
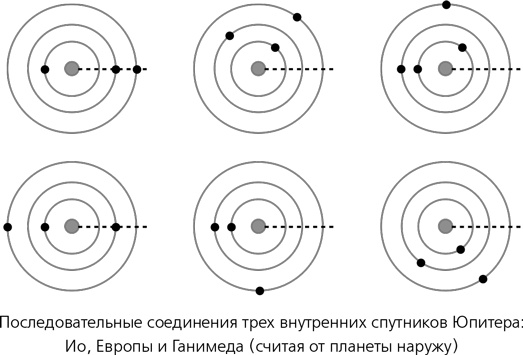
Спутники Юпитера стали для астрономов настоящей небесной лабораторией, впервые позволив наблюдать со стороны систему из нескольких тел. Ученые составляли таблицы движения этих тел, пытались это движение объяснять и предсказывать теоретически. Один из способов получить точные измерения — пронаблюдать транзит луны по диску планеты, потому что начало и конец транзита — четко определенные события. Затмения, когда луна, наоборот, заходит за планету, определяются не хуже. Джованни Годиерна отметил это в 1656 году, а примерно десятилетием позже Кассини начал длинную серию систематических наблюдений, в ходе которых отмечал также и другие совпадения, к примеру, соединения, при которых две луны выстраиваются в одну линию. К собственному удивлению, он обнаружил, что времена транзитов не согласуются с движением лун по правильным повторяющимся орбитам.
Датский астроном Оле Рёмер подхватил идею Галилея об определении долготы, и в 1671 году вместе с Жаном Пикаром провел наблюдения 140 затмений Ио в Ураниборге под Копенгагеном; в это же время Кассини наблюдал их в Париже. Сравнив временны́е отметки, астрономы вычислили разницу долгот двух обсерваторий. Кассини тогда уже обратил внимание на некоторые странности в наблюдениях и размышлял, не возникают ли они из-за того, что скорость света конечна. Рёмер свел воедино все наблюдения и выяснил, что очередные затмения наступали немного раньше, когда Земля находилась ближе к Юпитеру, и позднее, когда она находилась от него дальше. В 1676 году он сделал в Академии наук сообщение о причине этого явления: «Судя по всему, свету требуется около 10–11 минут, [чтобы пройти] расстояние, равное радиусу земной орбиты». Озвученное число основывалось на тщательных геометрических построениях, но наблюдения были не слишком точными; современное значение для этого интервала — 8 минут 19 секунд. Рёмер не опубликовал свои результаты в виде формальной научной работы, но его лекцию изложил — причем плохо — какой-то неизвестный репортер. Ученое сообщество приняло идею, согласно которой свет имеет конечную скорость, только в 1727 году.
Несмотря на все нерегулярности, Кассини ни разу не удалось наблюдать соединение сразу трех внутренних спутников (Ио, Европы и Ганимеда), когда все они одновременно выстраиваются в линию, совпадающую с лучом зрения; следовательно, что-то, вероятно, не позволяет им это сделать. Орбитальные периоды этих спутников соотносятся друг с другом приблизительно как 1:2:4, и в 1743 году Пер Варгентин, директор Стокгольмской обсерватории, показал, что это соотношение становится поразительно точным, если интерпретировать его заново, на этот раз корректно. Измеряя положение спутников как угол относительно некоторого фиксированного радиуса, он открыл следующую замечательную связь:
угол для Ио — 3 × угол для Европы + 2 × угол для Ганимеда = 180º.
Согласно его наблюдениям, это уравнение выполняется почти точно на длительных периодах времени, несмотря на нерегулярности орбит трех этих лун. Для соединения всех трех спутников нужно, чтобы все три угла были равны, но если это так, то в левой части приведенного уравнения мы получим 0º, а не 180º. Получается, что тройное соединение невозможно до тех пор, пока выполняется данное соотношение. Варгентин утверждал, что этого не произойдет еще по крайней мере 1,3 млн лет.
Из этого уравнения следует также, что соединения трех лун происходят в определенной повторяющейся последовательности:
Европа и Ганимед,
Ио и Ганимед,
Ио и Европа,
Ио и Ганимед,
Ио и Европа,
Ио и Ганимед.
Лаплас решил, что формула Варгентина не может быть простым совпадением и для такого соотношения должна быть конкретная динамическая причина. В 1784 году он вывел эту формулу из закона всемирного тяготения Ньютона. Из его вычислений следует, что на длительных интервалах времени комбинация соответствующих углов не остается равной в точности 180°; вместо этого наблюдается либрация — медленные колебания вокруг этой величины в обе стороны меньше чем на 1°. Это, конечно, достаточно мало, чтобы не допустить тройного соединения. Лаплас предсказал, что период этих колебаний должен составлять 2270 суток. Наблюдаемое значение на сегодняшний день — 2071 сутки — совсем неплохо. В его честь данное соотношение между тремя углами назвали резонансом Лапласа. Успех Лапласа стал весомым подтверждением закона Ньютона.
Мы сегодня знаем, почему во временах транзита наблюдается нерегулярность. Тяготение Юпитера вызывает прецессию приближенно эллиптических орбит его спутников (аналогично прецессии орбиты Меркурия вокруг Солнца), так что положение периовия — ближайшей к Юпитеру точки орбиты — изменяется довольно быстро. В формуле резонанса Лапласа прецессии компенсируют друг друга, но на индивидуальные транзиты влияют сильно.
Резонансом Лапласа называется любое подобное соотношение углов. Так, звезда Gliese 876 имеет систему экзопланет, первая из которых была обнаружена в 1998 году. В настоящее время известны четыре планеты, и три из них — Глизе 876c, Глизе 876b и Глизе 876e — имеют орбитальные периоды, равные 30,008; 61,116 и 124,26 суток, что подозрительно близко к соотношению 1:2:4. В 2010 году Эухенио Ривера с коллегами показали, что в данном случае наблюдается соотношение:
угол для 876c — 3 × угол для 876b + 2 × угол для 876e = 0°,
но сумма при колебаниях вокруг 0° отклоняется на целых 40°, то есть либрация здесь гораздо сильнее. В данном случае тройное соединение возможно, а почти соединение, близкое к тройному, происходит на каждом обороте внешней планеты. Моделирование показывает, что колебания вокруг 0° должны быть хаотичны, а период их составляет приблизительно 10 лет.
Три луны Плутона — Никта, Стикс и Гидра — тоже демонстрируют лапласоподобный резонанс, но здесь среднее соотношение периодов составляет 18:22:33, а среднее отношение орбит — 11:9:6. Уравнение здесь выглядит так:
3 × угол для Стикса — 5 × угол для Никты + 2 × угол для Гидры = 180°.



